# get rid of workspace
rm(list = ls())
# load packages
library(dplyr)
library(ggplot2)
library(readr)
library(kableExtra)
library(xpose4)
library(tidyr)
library(plotly)
# define base path
base_path <- paste0(here::here(), "/posts/understanding_nlme_estimation/")
# define function for html table output
mytbl <- function(tbl){
tbl |>
kable() |>
kable_styling()
}In this (somewhat lengthy) document I want to share my attempt at understanding and reproducing NONMEM’s objective function in R. Of course you can use NONMEM effectively without knowing the exact calculations behind the objective function and I did so myself for quite a while. But I believe that it’s helpful to have some understanding of what’s happening under the hood, even if it’s just to some extent. Calculating the objective function manually and understanding the math behind the estimation has always been on my bucket list, but I never really knew where to start. After getting some very helpful input during the PharMetrX (2024) A5 module, I felt ready to give it at least a try. So, here we are!
Let me briefly outline how I structured this document. The main goal is to manually calculate the objective function in R using straight line equations. Furthermore, I would like to visualize its 3D surface to see the path the estimation algorithm is taking. I also want to reproduce two key steps associated with the estimation: The COVARIANCE step to assess the parameter precision and the POSTHOC step to get individual parameter estimates. As we try to work through these calculations, I also aim to explore and explain to myself some of the theory and intuition behind concepts and calculations along the way.
To achieve this, we will first define a simple one-compartment pharmacokinetic model with intravenous bolus administration and first-order elimination (Section 2). Afterwards we will use this model to simulate some virtual concentration-time data (Section 3), which we will then fit using the Laplacian estimation (Section 4) to obtain a reference solution. I chose the Laplacian algorithm because it makes fewer assumptions and simplifications compared to FOCE or FO. It should be easier to go from Laplacian to FOCE-I than vice versa.
Then, in the biggest part of this document, we will try to construct the equations needed to calculate the objective function value for a given set of parameters and understand why we are taking each step (Section 5). After this is done, we will implement the functions in R (Section 6), reproduce each iteration of the NONMEM run and compare the results to the reference solution.
Finally, the reward for all the hard work: We will visualize the objective function surface in a 3D plot (Section 7). This should give us a better understanding of the search algorithm and the behavior of the objective function in dependence of the parameter estimates.
After that, we will attempt a complete estimation directly in R using the optim() function (Section 8) instead of only reproducing the objective function based on the iterations NONMEM took. We will compare our R-based parameter estimates against those obtained by NONMEM and discuss any differences.
Following this, we will mimick the COVARIANCE step by retrieving and inverting the Hessian matrix (Section 9) obtained during the R-based optimization to assess parameter precision (relative standard errors). In a last step, we will then calculate the individual ETAs by reproducing the POSTHOC step (Section 10) and comparing the results against NONMEM’s outputs.
A special thanks to Dr. Niklas Hartung for his input during the PharMetrX (2024) A5 module and his assistance while writing this blog post, Prof. Wilhelm Huisinga for his contributions during the module, and Dr. Christin Nyhoegen for the helpful discussions.
Before we get started, I want to note a few disclaimers to ward off any imposter syndrome that might kick in. I’m just a PhD student, not formally trained in mathematics or statistics, and I’m learning as I go. If you’re expecting an entirely error-free derivation with coherent statistical notation, this is not be the best resource. You better go with Wang (2007) in that case. My focus here is more about the intuition and maybe about developing a general understanding of the underlying processes.
Much of the content in this document is based on the work of others, and there’s not a lot of original thought here. I’ve relied heavily on several key publications (e.g., Wang (2007)), gained a lot of intuition from the PharMetrX (2024) A5 module, had important input from colleagues (see above) and used tools like Wolfram/Mathematica for some calculations and ChatGPT for parts of the writing. With that being said, let’s start!
As written above, we will try this exercise with one of the simplest model we can think of: A one-compartment PK model with i.v. bolus and first order elimination. Additionally, we are just considering to estimate two parameters: i) the typical clearance \(\theta_{TVCL}\) and ii) the inter-individual variability on clearance \(\omega^2\). The volume of distribution \(V_D\) and the residual unexplained variability \(\sigma^2\) are assumed to be fixed and known. Dealing with only two parameters should allow us to plot the surface of the objective function value in a 3D plot and it simplifies our lives a bit. Here is a little sketch of the model:
# Create the plot
ggplot() +
# Arrow for Dose (IV Bolus) -> Central Compartment
geom_segment(aes(x = 1, y = 2, xend = 2, yend = 2),
arrow = arrow(type = "closed", length = unit(0.3, "cm")),
color = "black") +
geom_text(aes(x = 1.5, y = 2.05, label = "Dose (i.v. bolus)"), size = 4) +
# Arrow for Central Compartment -> Clearance (CL + IIV)
geom_segment(aes(x = 3, y = 2, xend = 5, yend = 2),
arrow = arrow(type = "closed", length = unit(0.3, "cm")),
color = "black") +
geom_text(aes(x = 4.5, y = 2.05, label = "Clearance (+ IIV)"), size = 4) +
# Central Compartment (rectangle)
geom_rect(aes(xmin = 2, xmax = 4, ymin = 1.70, ymax = 2.30),
fill = "white", color = "black", size = 1.5) +
geom_text(aes(x = 3, y = 2, label = "Central Compartment"), size = 5) +
geom_text(aes(x = 3.85, y = 1.75, label = "VD"), size = 4) +
# Set limits and theme
xlim(1, 5) +
ylim(1.5, 2.5) +
theme_void() +
theme(
panel.grid = element_blank(),
plot.margin = unit(c(0,0,0,0), "cm"),
plot.background = element_rect(fill = "transparent", color = NA)
)
The first step is to define this model structure with some dummy parameter values inside NONMEM, which we will do now.
The NONMEM model code for our simple one-compartment PK model is shown below. Please note that we are using the ADVAN1 routine, which relies on the analytical expression for a one-compartment model, rather than an ODE solver.
1cmt_iv_sim.mod
# read_file(paste0(base_path, "/models/simulation/1cmt_iv_sim.mod"))
$PROBLEM 1cmt_iv_sim
$INPUT ID TIME EVID AMT RATE DV MDV
$DATA C:\Users\mklose\Desktop\G\Mitarbeiter\Klose\Miscellaneous\NLME_reproduction_R\data\input_for_sim\input_data.csv IGNORE=@
$SUBROUTINES ADVAN1 TRANS2
$PK
; define fixed effects parameters
CL = THETA(1) * EXP(ETA(1))
V = THETA(2)
; scaling
S1=V
$THETA
(0, 0.2, 1) ; 1 TVCL
3.15 FIX ; 2 TVV
$OMEGA
0.2 ; 1 OM_CL
$SIGMA
0.1 FIX ; 1 SIG_ADD
$ERROR
; add additive error
Y = F + EPS(1)
; store error for table output
ERR1 = EPS(1)
; $ESTIMATION METHOD=COND LAPLACIAN MAXEVAL=9999 SIGDIG=3 PRINT=1 NOABORT POSTHOC
$SIMULATION (12345678) ONLYSIM
$TABLE ID TIME EVID AMT RATE DV MDV ETA1 ERR1 NOAPPEND ONEHEADER NOPRINT FILE=sim_outDepending on the task (simulation vs. estimation), we’ll adjust the model code slightly. For simulation, we use $SIMULATION (12345678) ONLYSIM and for estimation, we are going to use $ESTIMATION METHOD=COND LAPLACIAN MAXEVAL=9999 SIGDIG=3 PRINT=1 NOABORT POSTHOC. Additionally, the $DATA block will vary depending on the task. For simulation, we will just pass a dosing and sampling scheme. For estimation, we’ll then use the simulated data from the first step and use the simulated concentration values for parameter estimation.
Okay, so far so good. We have our model in NONMEM and we also defined some dummy values for the parameter estimates. Now we want to simulate some virtual concentration-time data that will be used for model fitting later on. Typically you would have clinical data at hand, but we are just generating ourselves some clinical data to use for this exercise. We begin by constructing an input dataset that represents our dosing and sampling scheme, then simulate the concentration-time profiles, and finally visualize the pharmacokinetics to get a first understanding of the data.
To simulate data, we consider a scenario with 10 individuals, each having five observations at different time points within 24 hours. The selected time points are 0.01, 3, 6, 12, and 24 hours. To my understanding, it is crucial to have at least two observations per individual to reliably estimate inter-individual variability, as having only one observation per individual would make it impossible to distinguish between inter-individual variability and residual variability.
The dataset includes dosing records (EVID = 1) and observation records (EVID = 0). For now the dependent variable (DV) will be flagged to -99 since we will simulate these values in the following steps. Here is how our input dataset looks like:
# generate NONMEM input dataset for n individuals with 3 observations at different timepoints
n_ind <- 10
n_obs <- 5
timepoints <- c(0.01, 3, 6, 12, 24)
# observation events (EVID == 0)
obs_input <- tibble(
ID = rep(1:n_ind, each = n_obs),
TIME = rep(timepoints, n_ind),
EVID = 0,
AMT = 0,
RATE = 0,
DV = -99, # DV is what we want to simulate
MDV = 0
)
# dosing events (EVID == 1)
dosing_input <- tibble(
ID = rep(1:n_ind, each = 1),
TIME = 0,
EVID = 1,
AMT = 100,
RATE = 0,
DV = 0,
MDV = 1
)
# bind together and sort by ID and TIME
input_data <- bind_rows(obs_input, dosing_input) |>
arrange(ID, TIME)
# show input data
input_data |>
head(n=10) |>
mytbl()| ID | TIME | EVID | AMT | RATE | DV | MDV |
|---|---|---|---|---|---|---|
| 1 | 0.00 | 1 | 100 | 0 | 0 | 1 |
| 1 | 0.01 | 0 | 0 | 0 | -99 | 0 |
| 1 | 3.00 | 0 | 0 | 0 | -99 | 0 |
| 1 | 6.00 | 0 | 0 | 0 | -99 | 0 |
| 1 | 12.00 | 0 | 0 | 0 | -99 | 0 |
| 1 | 24.00 | 0 | 0 | 0 | -99 | 0 |
| 2 | 0.00 | 1 | 100 | 0 | 0 | 1 |
| 2 | 0.01 | 0 | 0 | 0 | -99 | 0 |
| 2 | 3.00 | 0 | 0 | 0 | -99 | 0 |
| 2 | 6.00 | 0 | 0 | 0 | -99 | 0 |
# save data to file
write_csv(input_data, paste0(base_path, "data/input_for_sim/input_data.csv"))
# write_csv(input_data, "C:\\Users\\mklose\\Desktop\\G\\Mitarbeiter\\Klose\\Miscellaneous\\NLME_reproduction_R\\data\\input_for_sim\\input_data.csv")We arbitrarily decided that each individual receives the same dose of 100 mg at time 0. Same dose fits all, right? We can see that at 0.01, 3, 6, 12, and 24 hours after dosing we encoded sampling events (EVID = 0). We can now plug this dataset into NONMEM and simulate these concentrations!
With the input dataset generated, the next step is to use it to simulate virtual concentration-time data. This simulation is performed using NONMEM, using the dosing and sampling dataset defined above. This step happens in NONMEM itself and will be be executed separately from this R session.
After running the simulation in NONMEM, the generated output (in our case a file called sim_out) contains the simulated concentration values within the DV column. The simulated dataset also includes additional columns such as ETA1, which represents the realization of inter-individual variability, and ERR1, which represents the realization of residual unexplained variability (RUV). So for each individual we have drawn one ETA1 and for each observation we have one ERR1.
# load simulated data
sim_data <- read_nm_table(paste0(base_path, "models/simulation/sim_out"))
# show simulated data
sim_data |>
head(n=10) |>
mytbl()| ID | TIME | EVID | AMT | RATE | DV | MDV | ETA1 | ERR1 |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.00 | 1 | 100 | 0 | 0.0000 | 1 | 0.39117 | 0.136050 |
| 1 | 0.01 | 0 | 0 | 0 | 30.8160 | 0 | 0.39117 | -0.900050 |
| 1 | 3.00 | 0 | 0 | 0 | 24.5520 | 0 | 0.39117 | 0.598410 |
| 1 | 6.00 | 0 | 0 | 0 | 17.9250 | 0 | 0.39117 | -0.148090 |
| 1 | 12.00 | 0 | 0 | 0 | 10.1100 | 0 | 0.39117 | -0.180050 |
| 1 | 24.00 | 0 | 0 | 0 | 3.5975 | 0 | 0.39117 | 0.262420 |
| 2 | 0.00 | 1 | 100 | 0 | 0.0000 | 1 | 0.12054 | -0.037607 |
| 2 | 0.01 | 0 | 0 | 0 | 31.4550 | 0 | 0.12054 | -0.268190 |
| 2 | 3.00 | 0 | 0 | 0 | 26.2030 | 0 | 0.12054 | 0.595370 |
| 2 | 6.00 | 0 | 0 | 0 | 20.5520 | 0 | 0.12054 | -0.103830 |
We can see that we obtained a dataset with the simulated concentration values in the DV column. The simulated data now needs to be saved as .csv in order to use it in the subsequent steps within NONMEM.
# subset dataframe
sim_data_reduced <- sim_data |>
select(ID, TIME, EVID, AMT, RATE, DV, MDV)
# save dataframe
write_csv(sim_data_reduced, paste0(base_path, "data/output_from_sim/sim_data.csv"))
# filter to have EVID == 0 only
sim_data_reduced <- sim_data_reduced |>
filter(EVID == 0) Great! The sim_data.csv dataframe was successfully saved and we can later use it for the generation of the reference solution in NONMEM.
Now we can visualize the simulated data stratified by individual to get a feeling for our virtual clinical data.
# show individual profiles
sim_data |>
filter(EVID == 0) |>
ggplot(aes(x=TIME, y=DV, group=ID, color=as.factor(ID))) +
geom_point()+
geom_line()+
theme_bw()+
scale_y_continuous(limits=c(0,NA))+
labs(x="Time after last dose [h]", y="Concentration [mg/L]")+
ggtitle("Simulated data")+
scale_color_discrete("Individual")
As each of the 10 individuals received the same dose, we can clearly see the impact of variability on clearance on concentration-time profiles. Additionally, the single data points are influenced by the residual unexplained variability, which adds noise to the readouts.
We are making progress! In a next step we now want to generate a reference solution for the estimation within NONMEM. By doing so we can (in the end) compare our own implementation of the objective function to the one NONMEM uses.
The idea is now to use the virtual clinical data we have generated in the last step to perform an estimation step using the Laplacian estimation algorithm in NONMEM. This will serve as some kind of reference solution, so we are able to compare the results of our own implementation with the NONMEM output. We are going to use the same model which was used to simulate the data, but this time we are using it for a estimation problem. Therefore, we are going to change the $ESTIMATION block in the model code (see Section 2.1) to: $ESTIMATION METHOD=COND LAPLACIAN MAXEVAL=9999 SIGDIG=3 PRINT=1 NOABORT POSTHOC.
As mentioned before, the actual estimation will again happen in NONMEM and therefore needs to be executed separately from this R session. In this step, we are just going to read in the NONMEM output files and visualize them appropriately. This is going to happen as a next step.
First of all, we can read in the .lst file. It contains many information about the parameter estimation process and is a nice way to get a quick overview of the model run.
read_file(paste0(base_path, "models/estimation/1cmt_iv_est.lst"))1cmt_iv_sim.lst
Mon 12/30/2024
10:54 PM
$PROBLEM 1cmt_iv_est
$INPUT ID TIME EVID AMT RATE DV MDV
$DATA sim_data.csv IGNORE=@
$SUBROUTINE ADVAN1 TRANS2
$PK
; define fixed effects parameters
CL = THETA(1) * EXP(ETA(1))
V = THETA(2)
; scaling
S1=V
$THETA (0,0.1,1) ; 1 TVCL
3.15 FIX ; 2 TVV
$OMEGA 0.15 ; 1 OM_CL
$SIGMA 0.1 FIX ; 1 SIG_ADD
$ERROR
; add additive error
Y = F + EPS(1)
; store error for table output
ERR1 = EPS(1)
$ESTIMATION METHOD=COND LAPLACIAN MAXEVAL=9999 SIGDIG=3 PRINT=1
NOABORT POSTHOC
$COVARIANCE PRINT=E
$TABLE ID TIME EVID AMT RATE DV MDV ETA1 ERR1 CL NOAPPEND
ONEHEADER NOPRINT FILE=estim_out
NM-TRAN MESSAGES
WARNINGS AND ERRORS (IF ANY) FOR PROBLEM 1
(WARNING 2) NM-TRAN INFERS THAT THE DATA ARE POPULATION.
License Registered to: Freie Universitaet Berlin Department of Clinical Pharmacy Biochemistry
Expiration Date: 14 JAN 2025
Current Date: 30 DEC 2024
**** WARNING!!! Days until program expires : 19 ****
**** CONTACT idssoftware@iconplc.com FOR RENEWAL ****
1NONLINEAR MIXED EFFECTS MODEL PROGRAM (NONMEM) VERSION 7.5.1
ORIGINALLY DEVELOPED BY STUART BEAL, LEWIS SHEINER, AND ALISON BOECKMANN
CURRENT DEVELOPERS ARE ROBERT BAUER, ICON DEVELOPMENT SOLUTIONS,
AND ALISON BOECKMANN. IMPLEMENTATION, EFFICIENCY, AND STANDARDIZATION
PERFORMED BY NOUS INFOSYSTEMS.
PROBLEM NO.: 1
1cmt_iv_est
0DATA CHECKOUT RUN: NO
DATA SET LOCATED ON UNIT NO.: 2
THIS UNIT TO BE REWOUND: NO
NO. OF DATA RECS IN DATA SET: 60
NO. OF DATA ITEMS IN DATA SET: 7
ID DATA ITEM IS DATA ITEM NO.: 1
DEP VARIABLE IS DATA ITEM NO.: 6
MDV DATA ITEM IS DATA ITEM NO.: 7
0INDICES PASSED TO SUBROUTINE PRED:
3 2 4 5 0 0 0 0 0 0 0
0LABELS FOR DATA ITEMS:
ID TIME EVID AMT RATE DV MDV
0(NONBLANK) LABELS FOR PRED-DEFINED ITEMS:
CL ERR1
0FORMAT FOR DATA:
(7E8.0)
TOT. NO. OF OBS RECS: 50
TOT. NO. OF INDIVIDUALS: 10
0LENGTH OF THETA: 2
0DEFAULT THETA BOUNDARY TEST OMITTED: NO
0OMEGA HAS SIMPLE DIAGONAL FORM WITH DIMENSION: 1
0DEFAULT OMEGA BOUNDARY TEST OMITTED: NO
0SIGMA HAS SIMPLE DIAGONAL FORM WITH DIMENSION: 1
0DEFAULT SIGMA BOUNDARY TEST OMITTED: NO
0INITIAL ESTIMATE OF THETA:
LOWER BOUND INITIAL EST UPPER BOUND
0.0000E+00 0.1000E+00 0.1000E+01
0.3150E+01 0.3150E+01 0.3150E+01
0INITIAL ESTIMATE OF OMEGA:
0.1500E+00
0INITIAL ESTIMATE OF SIGMA:
0.1000E+00
0SIGMA CONSTRAINED TO BE THIS INITIAL ESTIMATE
0COVARIANCE STEP OMITTED: NO
EIGENVLS. PRINTED: YES
SPECIAL COMPUTATION: NO
COMPRESSED FORMAT: NO
GRADIENT METHOD USED: NOSLOW
SIGDIGITS ETAHAT (SIGLO): -1
SIGDIGITS GRADIENTS (SIGL): -1
EXCLUDE COV FOR FOCE (NOFCOV): NO
Cholesky Transposition of R Matrix (CHOLROFF):0
KNUTHSUMOFF: -1
RESUME COV ANALYSIS (RESUME): NO
SIR SAMPLE SIZE (SIRSAMPLE):
NON-LINEARLY TRANSFORM THETAS DURING COV (THBND): 1
PRECONDTIONING CYCLES (PRECOND): 0
PRECONDTIONING TYPES (PRECONDS): TOS
FORCED PRECONDTIONING CYCLES (PFCOND):0
PRECONDTIONING TYPE (PRETYPE): 0
FORCED POS. DEFINITE SETTING DURING PRECONDITIONING: (FPOSDEF):0
SIMPLE POS. DEFINITE SETTING: (POSDEF):-1
0TABLES STEP OMITTED: NO
NO. OF TABLES: 1
SEED NUMBER (SEED): 11456
NPDTYPE: 0
INTERPTYPE: 0
RANMETHOD: 3U
MC SAMPLES (ESAMPLE): 300
WRES SQUARE ROOT TYPE (WRESCHOL): EIGENVALUE
0-- TABLE 1 --
0RECORDS ONLY: ALL
04 COLUMNS APPENDED: NO
PRINTED: NO
HEADER: YES
FILE TO BE FORWARDED: NO
FORMAT: S1PE11.4
IDFORMAT:
LFORMAT:
RFORMAT:
FIXED_EFFECT_ETAS:
0USER-CHOSEN ITEMS:
ID TIME EVID AMT RATE DV MDV ETA1 ERR1 CL
1DOUBLE PRECISION PREDPP VERSION 7.5.1
ONE COMPARTMENT MODEL (ADVAN1)
0MAXIMUM NO. OF BASIC PK PARAMETERS: 2
0BASIC PK PARAMETERS (AFTER TRANSLATION):
ELIMINATION RATE (K) IS BASIC PK PARAMETER NO.: 1
TRANSLATOR WILL CONVERT PARAMETERS
CLEARANCE (CL) AND VOLUME (V) TO K (TRANS2)
0COMPARTMENT ATTRIBUTES
COMPT. NO. FUNCTION INITIAL ON/OFF DOSE DEFAULT DEFAULT
STATUS ALLOWED ALLOWED FOR DOSE FOR OBS.
1 CENTRAL ON NO YES YES YES
2 OUTPUT OFF YES NO NO NO
1
ADDITIONAL PK PARAMETERS - ASSIGNMENT OF ROWS IN GG
COMPT. NO. INDICES
SCALE BIOAVAIL. ZERO-ORDER ZERO-ORDER ABSORB
FRACTION RATE DURATION LAG
1 3 * * * *
2 * - - - -
- PARAMETER IS NOT ALLOWED FOR THIS MODEL
* PARAMETER IS NOT SUPPLIED BY PK SUBROUTINE;
WILL DEFAULT TO ONE IF APPLICABLE
0DATA ITEM INDICES USED BY PRED ARE:
EVENT ID DATA ITEM IS DATA ITEM NO.: 3
TIME DATA ITEM IS DATA ITEM NO.: 2
DOSE AMOUNT DATA ITEM IS DATA ITEM NO.: 4
DOSE RATE DATA ITEM IS DATA ITEM NO.: 5
0PK SUBROUTINE CALLED WITH EVERY EVENT RECORD.
PK SUBROUTINE NOT CALLED AT NONEVENT (ADDITIONAL OR LAGGED) DOSE TIMES.
0ERROR SUBROUTINE CALLED WITH EVERY EVENT RECORD.
1
#TBLN: 1
#METH: Laplacian Conditional Estimation
ESTIMATION STEP OMITTED: NO
ANALYSIS TYPE: POPULATION
NUMBER OF SADDLE POINT RESET ITERATIONS: 0
GRADIENT METHOD USED: NOSLOW
CONDITIONAL ESTIMATES USED: YES
CENTERED ETA: NO
EPS-ETA INTERACTION: NO
LAPLACIAN OBJ. FUNC.: YES
NUMERICAL 2ND DERIVATIVES: NO
NO. OF FUNCT. EVALS. ALLOWED: 9999
NO. OF SIG. FIGURES REQUIRED: 3
INTERMEDIATE PRINTOUT: YES
ESTIMATE OUTPUT TO MSF: NO
ABORT WITH PRED EXIT CODE 1: NO
IND. OBJ. FUNC. VALUES SORTED: NO
NUMERICAL DERIVATIVE
FILE REQUEST (NUMDER): NONE
MAP (ETAHAT) ESTIMATION METHOD (OPTMAP): 0
ETA HESSIAN EVALUATION METHOD (ETADER): 0
INITIAL ETA FOR MAP ESTIMATION (MCETA): 0
SIGDIGITS FOR MAP ESTIMATION (SIGLO): 100
GRADIENT SIGDIGITS OF
FIXED EFFECTS PARAMETERS (SIGL): 100
NOPRIOR SETTING (NOPRIOR): 0
NOCOV SETTING (NOCOV): OFF
DERCONT SETTING (DERCONT): OFF
FINAL ETA RE-EVALUATION (FNLETA): 1
EXCLUDE NON-INFLUENTIAL (NON-INFL.) ETAS
IN SHRINKAGE (ETASTYPE): NO
NON-INFL. ETA CORRECTION (NONINFETA): 0
RAW OUTPUT FILE (FILE): psn.ext
EXCLUDE TITLE (NOTITLE): NO
EXCLUDE COLUMN LABELS (NOLABEL): NO
FORMAT FOR ADDITIONAL FILES (FORMAT): S1PE12.5
PARAMETER ORDER FOR OUTPUTS (ORDER): TSOL
KNUTHSUMOFF: 0
INCLUDE LNTWOPI: NO
INCLUDE CONSTANT TERM TO PRIOR (PRIORC): NO
INCLUDE CONSTANT TERM TO OMEGA (ETA) (OLNTWOPI):NO
ADDITIONAL CONVERGENCE TEST (CTYPE=4)?: NO
EM OR BAYESIAN METHOD USED: NONE
THE FOLLOWING LABELS ARE EQUIVALENT
PRED=NPRED
RES=NRES
WRES=NWRES
IWRS=NIWRES
IPRD=NIPRED
IRS=NIRES
MONITORING OF SEARCH:
0ITERATION NO.: 0 OBJECTIVE VALUE: 41.8454368139310 NO. OF FUNC. EVALS.: 4
CUMULATIVE NO. OF FUNC. EVALS.: 4
NPARAMETR: 1.0000E-01 1.5000E-01
PARAMETER: 1.0000E-01 1.0000E-01
GRADIENT: -1.0545E+02 -1.0294E+02
0ITERATION NO.: 1 OBJECTIVE VALUE: -2.74307593433339 NO. OF FUNC. EVALS.: 5
CUMULATIVE NO. OF FUNC. EVALS.: 9
NPARAMETR: 1.6837E-01 4.8397E-01
PARAMETER: 7.0000E-01 6.8569E-01
GRADIENT: 2.8868E+00 9.4212E+00
0ITERATION NO.: 2 OBJECTIVE VALUE: -3.06819849357734 NO. OF FUNC. EVALS.: 8
CUMULATIVE NO. OF FUNC. EVALS.: 17
NPARAMETR: 1.6369E-01 3.8814E-01
PARAMETER: 6.6620E-01 5.7537E-01
GRADIENT: -2.2554E+00 5.6641E+00
0ITERATION NO.: 3 OBJECTIVE VALUE: -11.2971148236422 NO. OF FUNC. EVALS.: 5
CUMULATIVE NO. OF FUNC. EVALS.: 22
NPARAMETR: 2.1655E-01 1.4655E-01
PARAMETER: 1.0114E+00 8.8367E-02
GRADIENT: 6.6259E+00 2.6609E+00
0ITERATION NO.: 4 OBJECTIVE VALUE: -11.2971148236422 NO. OF FUNC. EVALS.: 10
CUMULATIVE NO. OF FUNC. EVALS.: 32
NPARAMETR: 2.1655E-01 1.4655E-01
PARAMETER: 1.0114E+00 8.8367E-02
GRADIENT: -1.3899E+01 2.6592E+00
0ITERATION NO.: 5 OBJECTIVE VALUE: -12.4187275503686 NO. OF FUNC. EVALS.: 7
CUMULATIVE NO. OF FUNC. EVALS.: 39
NPARAMETR: 2.5349E-01 8.6243E-02
PARAMETER: 1.2172E+00 -1.7673E-01
GRADIENT: 4.7000E+00 -5.6454E+00
0ITERATION NO.: 6 OBJECTIVE VALUE: -12.7891181563899 NO. OF FUNC. EVALS.: 7
CUMULATIVE NO. OF FUNC. EVALS.: 46
NPARAMETR: 2.4329E-01 1.1715E-01
PARAMETER: 1.1625E+00 -2.3573E-02
GRADIENT: -1.7854E+00 1.1790E+00
0ITERATION NO.: 7 OBJECTIVE VALUE: -12.8236151522707 NO. OF FUNC. EVALS.: 7
CUMULATIVE NO. OF FUNC. EVALS.: 53
NPARAMETR: 2.4614E-01 1.1120E-01
PARAMETER: 1.1779E+00 -4.9675E-02
GRADIENT: -2.9776E-01 2.0940E-01
0ITERATION NO.: 8 OBJECTIVE VALUE: -12.8245888793110 NO. OF FUNC. EVALS.: 7
CUMULATIVE NO. OF FUNC. EVALS.: 60
NPARAMETR: 2.4672E-01 1.0995E-01
PARAMETER: 1.1810E+00 -5.5291E-02
GRADIENT: 1.8561E-02 -1.2024E-02
0ITERATION NO.: 9 OBJECTIVE VALUE: -12.8245933812655 NO. OF FUNC. EVALS.: 7
CUMULATIVE NO. OF FUNC. EVALS.: 67
NPARAMETR: 2.4668E-01 1.1002E-01
PARAMETER: 1.1808E+00 -5.4985E-02
GRADIENT: -1.3169E-04 1.3509E-04
0ITERATION NO.: 10 OBJECTIVE VALUE: -12.8245933812655 NO. OF FUNC. EVALS.: 4
CUMULATIVE NO. OF FUNC. EVALS.: 71
NPARAMETR: 2.4668E-01 1.1002E-01
PARAMETER: 1.1808E+00 -5.4985E-02
GRADIENT: -1.3169E-04 1.3509E-04
#TERM:
0MINIMIZATION SUCCESSFUL
NO. OF FUNCTION EVALUATIONS USED: 71
NO. OF SIG. DIGITS IN FINAL EST.: 4.5
ETABAR IS THE ARITHMETIC MEAN OF THE ETA-ESTIMATES,
AND THE P-VALUE IS GIVEN FOR THE NULL HYPOTHESIS THAT THE TRUE MEAN IS 0.
ETABAR: -1.8954E-05
SE: 1.0473E-01
N: 10
P VAL.: 9.9986E-01
ETASHRINKSD(%) 1.5107E-01
ETASHRINKVR(%) 3.0192E-01
EBVSHRINKSD(%) 1.3728E-01
EBVSHRINKVR(%) 2.7437E-01
RELATIVEINF(%) 9.9726E+01
EPSSHRINKSD(%) 1.8336E+01
EPSSHRINKVR(%) 3.3311E+01
TOTAL DATA POINTS NORMALLY DISTRIBUTED (N): 50
N*LOG(2PI) CONSTANT TO OBJECTIVE FUNCTION: 91.893853320467272
OBJECTIVE FUNCTION VALUE WITHOUT CONSTANT: -12.824593381265490
OBJECTIVE FUNCTION VALUE WITH CONSTANT: 79.069259939201785
REPORTED OBJECTIVE FUNCTION DOES NOT CONTAIN CONSTANT
TOTAL EFFECTIVE ETAS (NIND*NETA): 10
#TERE:
Elapsed estimation time in seconds: 0.02
Elapsed covariance time in seconds: 0.00
Elapsed postprocess time in seconds: 0.00
1
************************************************************************************************************************
******************** ********************
******************** LAPLACIAN CONDITIONAL ESTIMATION ********************
#OBJT:************** MINIMUM VALUE OF OBJECTIVE FUNCTION ********************
******************** ********************
************************************************************************************************************************
#OBJV:******************************************** -12.825 **************************************************
1
************************************************************************************************************************
******************** ********************
******************** LAPLACIAN CONDITIONAL ESTIMATION ********************
******************** FINAL PARAMETER ESTIMATE ********************
******************** ********************
************************************************************************************************************************
THETA - VECTOR OF FIXED EFFECTS PARAMETERS *********
TH 1 TH 2
2.47E-01 3.15E+00
OMEGA - COV MATRIX FOR RANDOM EFFECTS - ETAS ********
ETA1
ETA1
+ 1.10E-01
SIGMA - COV MATRIX FOR RANDOM EFFECTS - EPSILONS ****
EPS1
EPS1
+ 1.00E-01
1
OMEGA - CORR MATRIX FOR RANDOM EFFECTS - ETAS *******
ETA1
ETA1
+ 3.32E-01
SIGMA - CORR MATRIX FOR RANDOM EFFECTS - EPSILONS ***
EPS1
EPS1
+ 3.16E-01
1
************************************************************************************************************************
******************** ********************
******************** LAPLACIAN CONDITIONAL ESTIMATION ********************
******************** STANDARD ERROR OF ESTIMATE ********************
******************** ********************
************************************************************************************************************************
THETA - VECTOR OF FIXED EFFECTS PARAMETERS *********
TH 1 TH 2
2.59E-02 .........
OMEGA - COV MATRIX FOR RANDOM EFFECTS - ETAS ********
ETA1
ETA1
+ 4.87E-02
SIGMA - COV MATRIX FOR RANDOM EFFECTS - EPSILONS ****
EPS1
EPS1
+ .........
1
OMEGA - CORR MATRIX FOR RANDOM EFFECTS - ETAS *******
ETA1
ETA1
+ 7.35E-02
SIGMA - CORR MATRIX FOR RANDOM EFFECTS - EPSILONS ***
EPS1
EPS1
+ .........
1
************************************************************************************************************************
******************** ********************
******************** LAPLACIAN CONDITIONAL ESTIMATION ********************
******************** COVARIANCE MATRIX OF ESTIMATE ********************
******************** ********************
************************************************************************************************************************
TH 1 TH 2 OM11 SG11
TH 1
+ 6.72E-04
TH 2
+ ......... .........
OM11
+ 7.98E-04 ......... 2.37E-03
SG11
+ ......... ......... ......... .........
1
************************************************************************************************************************
******************** ********************
******************** LAPLACIAN CONDITIONAL ESTIMATION ********************
******************** CORRELATION MATRIX OF ESTIMATE ********************
******************** ********************
************************************************************************************************************************
TH 1 TH 2 OM11 SG11
TH 1
+ 2.59E-02
TH 2
+ ......... .........
OM11
+ 6.32E-01 ......... 4.87E-02
SG11
+ ......... ......... ......... .........
1
************************************************************************************************************************
******************** ********************
******************** LAPLACIAN CONDITIONAL ESTIMATION ********************
******************** INVERSE COVARIANCE MATRIX OF ESTIMATE ********************
******************** ********************
************************************************************************************************************************
TH 1 TH 2 OM11 SG11
TH 1
+ 2.48E+03
TH 2
+ ......... .........
OM11
+ -8.32E+02 ......... 7.01E+02
SG11
+ ......... ......... ......... .........
1
************************************************************************************************************************
******************** ********************
******************** LAPLACIAN CONDITIONAL ESTIMATION ********************
******************** EIGENVALUES OF COR MATRIX OF ESTIMATE ********************
******************** ********************
************************************************************************************************************************
1 2
3.68E-01 1.63E+00
Elapsed finaloutput time in seconds: 0.01
#CPUT: Total CPU Time in Seconds, 0.016
Stop Time:
Mon 12/30/2024
10:54 PMIt is still quite a long file and a lot of text, that’s why the output is collapsed.
As a next step we can run the PsN sumo command to get a quick run summary. It tells us if the minimization was successful, if there has been any rounding errors, zero gradients, and so on.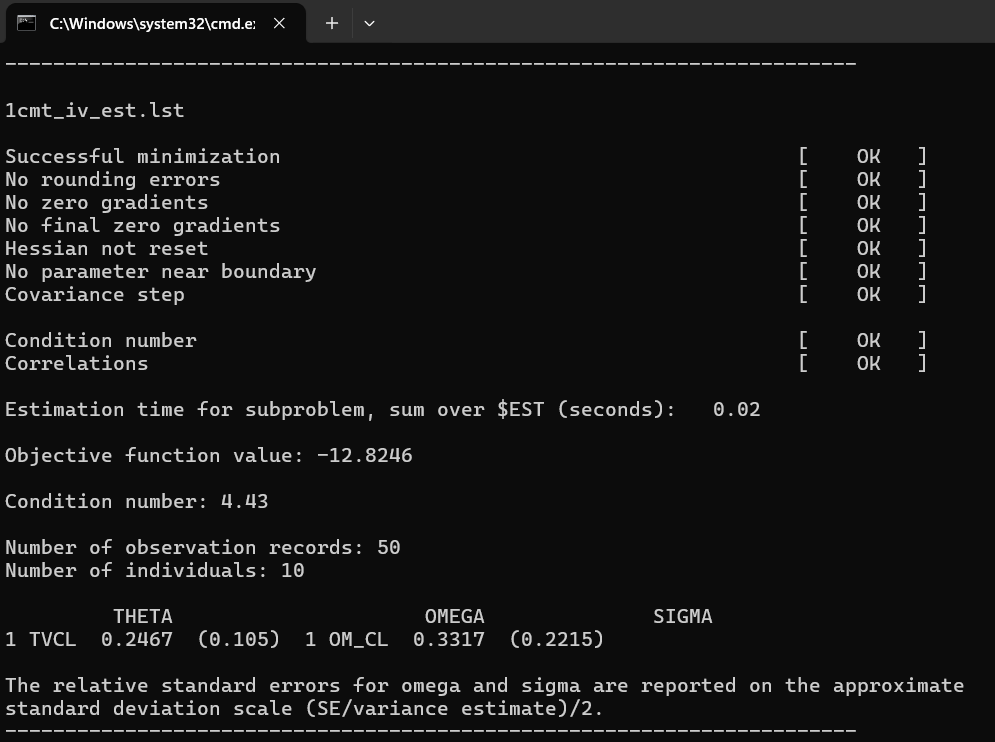
In this screenshot we can also already see our maximum likelihood estimates for THETA and OMEGA and their associated relative standard errors.
But which steps did the NONMEM algorithm take to end up in the maximum likelihood estimate? We can read in the .ext file, which contains information about the iterations of the estimation process and also the objective function value at each iteration. Here is how it looks like:
# Read the data, skipping the first line
ext_file <- read_table(paste0(base_path, "models/estimation/1cmt_iv_est.ext"), skip = 1)
# keep only positive iterations
ext_file <- ext_file |>
filter(ITERATION >= 0)
# rename columns
ext_file <- ext_file |>
rename(
CL = "THETA1",
V = "THETA2",
RUV_VAR = "SIGMA(1,1)",
IIV_VAR = "OMEGA(1,1)"
)
# Show the tibble
ext_file |>
head(n=10) |>
mytbl()| ITERATION | CL | V | RUV_VAR | IIV_VAR | OBJ |
|---|---|---|---|---|---|
| 0 | 0.100000 | 3.15 | 0.1 | 0.1500000 | 41.845437 |
| 1 | 0.168370 | 3.15 | 0.1 | 0.4839690 | -2.743076 |
| 2 | 0.163689 | 3.15 | 0.1 | 0.3881430 | -3.068198 |
| 3 | 0.216552 | 3.15 | 0.1 | 0.1465500 | -11.297115 |
| 4 | 0.216552 | 3.15 | 0.1 | 0.1465500 | -11.297115 |
| 5 | 0.253493 | 3.15 | 0.1 | 0.0862428 | -12.418728 |
| 6 | 0.243287 | 3.15 | 0.1 | 0.1171540 | -12.789118 |
| 7 | 0.246139 | 3.15 | 0.1 | 0.1111950 | -12.823615 |
| 8 | 0.246715 | 3.15 | 0.1 | 0.1099530 | -12.824589 |
| 9 | 0.246682 | 3.15 | 0.1 | 0.1100200 | -12.824593 |
In total, we have 10 entries/rows in the .ext file. The first row, iteration 0, contains the initial estimates (which we have provided in the model code) and its associated objective function value. Then we have iterations 1-8, which are intermediate steps. Finally, we are going to end up in iteration 9, at which point the convergence criterium was fulfilled and the estimation process has ended.
The columns carry the following information:
We can use this output file to visualize the change in parameter values and objective function value over the iteration number, so we get a better understanding what is going on during the estimation steps:
# Visualize
ext_file |>
pivot_longer(cols = c(CL, V, RUV_VAR, IIV_VAR, OBJ), names_to = "parameter", values_to = "value") |>
ggplot(aes(x=ITERATION, y=value))+
geom_line()+
geom_point()+
facet_wrap(~parameter, scales="free")+
theme_bw()+
labs(x="Iteration", y="Estimation diagnostic")+
ggtitle("Estimation diagnostics over iterations")
In this exercise, the reproduction of the objective function value for a given set of parameters will be the main goal and this .ext file provides us with the reference solution. I actually don’t want to go down the rabbit hole of trying to reproduce the math behind these optimization algorithms. However, in Section 8, we are going to at least use the optim function in R to partly reproduce the search algorithm.
In the next big chapter we will try to understand the theory behind calculating the log-likelihood needed for the objective function based on our simple example.
In our little example we assume to have a (simple) hierarchical nonlinear mixed-effects (NLME) model, for which we want to conduct the parameter estimation. To my understanding the hierarchical structure is given by having variability defined on a population (=parameter) level and an individual (=observation) level, while the individual level depends on the parameter level. Let’s have a closer look to both of these levels.
The population level is represented by an inter-individual variability (IIV) term, which assumes a log-normal distribution around a typical parameter value. In this simplified example we only consider IIV on clearance and do not consider any other random effects. The population (or parameter) level can be defined as follows:
\[CL_i = \theta_{TVCL} \cdot e^{\eta_{i}},~~~~~\eta_{i} \sim N(0, \omega^2) \tag{1}\]
Here, the individual clearance (\(CL_i\)) is modeled as a log-normally distributed parameter, where (\(\theta_{\text{TVCL}}\)) is the typical clearance value and \(\eta_{i}\) is a random effect accounting for inter-individual variability (IIV). We assume that this random effect follows a normal distribution with mean zero and variance \(\omega^2\). An example plot of such a population level is shown below:
# Set seed for reproducibility
set.seed(123)
# Define population parameters
theta_TVCL <- 10 # Typical clearance (L/h)
omega_sq <- 0.2 # Variance of IIV on clearance
omega <- sqrt(omega_sq) # Standard deviation of IIV
num_individuals <- 5000 # Number of individuals in the population
# Simulate individual random effects
eta_i <- rnorm(num_individuals, mean = 0, sd = omega)
# Compute individual clearances
CL_i <- theta_TVCL * exp(eta_i)
# Create a data frame for plotting
population_data <- data.frame(
Individual = 1:num_individuals,
eta_i = eta_i,
CL = CL_i
)
# Calculate density for annotation placement
density_CL <- density(CL_i)
max_density <- max(density_CL$y)
# Create the ggplot
p_pop <- ggplot(population_data, aes(x = CL)) +
# Histogram of clearance values
geom_histogram(aes(y = ..density..), binwidth = 0.5, fill = "lightgreen", color = "black", alpha = 0.7) +
# Density curve
geom_density(color = "darkgreen", size = 1) +
# Vertical line for typical clearance
geom_vline(xintercept = theta_TVCL, color = "blue", linetype = "dashed", size = 1) +
# Labels and theme
labs(
title = "Population level: Clearance",
x = "Clearance (L/h)",
y = "Density"
) +
theme_bw() +
# Annotation for Typical Clearance
annotate("text", x = theta_TVCL + 5, y = max_density * 0.9,
label = expression(theta[TVCL]~": Typical Clearance"),
color = "blue", hjust = 0) +
geom_segment(aes(x = theta_TVCL + 5, y = max_density * 0.9,
xend = theta_TVCL, yend = max_density * 0.8),
arrow = arrow(length = unit(0.2, "cm")), color = "blue") +
# Annotation for IIV
annotate("text", x = theta_TVCL + 13, y = max_density * 0.6,
label = expression(IIV~"("~omega^2~")"),
color = "darkgreen", hjust = 0.5) +
geom_segment(aes(x = theta_TVCL + 10, y = max_density * 0.6,
xend = theta_TVCL+3, yend = max_density * 0.55),
arrow = arrow(length = unit(0.2, "cm")), color = "darkgreen")
# Display the plot
print(p_pop)
This plot represents the population level of our model, where the clearance values are sampled from a log-normal distribution around the typical clearance value. The dashed line represents the typical clearance value \(\theta_{TVCL}\), and the green curve/bars represents the distribution of clearances in the population.
The random effect \(\eta_i\) itself follows a normal distribution \(N(0, \omega^2)\) and is visualized below:
# plot histogram
population_data |>
ggplot(aes(x=eta_i)) +
geom_histogram(aes(y = ..density..), color="black", fill="lightblue", binwidth = 0.05, alpha=0.7) +
labs(x="ETA", y = "Density", title = "Population level: ETA",)+
geom_vline(xintercept = 0, linetype = "dashed", linewidth = 1)+
theme_bw()
The individual level on the other hand is defined by the observed and predicted concentrations for each subject. The predictions are based on the structural model and dependent on the individual parameters (which can be treated as a random variable, in our case CL). The individual level also incorporates residual unexplained variability (RUV), which distribution tells us how to define the likelihood function in the end. The individual level can be defined by:
\[Y_{ij} \mid CL_i = f(x_{ij}; CL_i) + \epsilon_{ij},~~~~~\epsilon_{ij} \sim N(0, \sigma^2) \tag{2}\] where we can note that:
In our example we have two random variables, \(Y_{ij}\) and \(CL_i\), with parameters \(\beta := (\theta_{TVCL}, \omega^2, \sigma^2)\). In our example we just want to estimate the typical clearance \(\theta_{TVCL}\) and the IIV on clearance \(\omega^2\). The residual unexplained variability \(\sigma^2\) is assumed to be known and fixed. The individual level with RUV is illustrated below:
# Set seed for reproducibility
set.seed(123)
# Define model parameters
theta_TVCL <- 10 # Typical clearance (L/h)
omega <- 0.447 # IIV on clearance (sqrt(omega^2) where omega^2 = 0.2)
sigma <- 0.5 # Residual unexplained variability (standard deviation)
V <- 20 # Volume of distribution (L)
Dose <- 100 # Dose administered (mg)
# Simulate data for one individual
individual_id <- 1
eta_i <- rnorm(1, mean = 0, sd = omega) # Individual random effect
CL_i <- theta_TVCL * exp(eta_i) # Individual clearance
# Define time points
time <- seq(0, 10, by = 1) # From 0 to 10 hours
# Compute predicted concentrations based on the 1 cmt model
C_pred <- (Dose / V) * exp(- (CL_i / V) * time)
# Add residual unexplained variability
epsilon_ij <- rnorm(length(time), mean = 0, sd = sigma)
C_obs <- C_pred + epsilon_ij
# Create a data frame
ind_lvl_data <- data.frame(
Time = time,
Predicted = C_pred,
Observed = C_obs
)
# Compute the upper and lower bounds for the normal distribution around prediction
ind_lvl_data <- ind_lvl_data |>
mutate(
Upper = Predicted + sigma,
Lower = Predicted - sigma
)
# Create the ggplot
p <- ggplot(ind_lvl_data, aes(x = Time)) +
# Shaded area for normal distribution around prediction
geom_ribbon(aes(ymin = Lower, ymax = Upper), fill = "lightblue", alpha = 0.5) +
# Predicted concentration line
geom_line(aes(y = Predicted), color = "black", size = 1) +
# Observed data points
geom_point(aes(y = Observed), color = "red", size = 2) +
# Labels and theme
labs(
title = "Individual level",
x = "Time (hours)",
y = "Concentration (mg/L)"
) +
theme_bw() +
# Adjusted annotation for f(x)
annotate("text", x = 6, y = 1.8, label = "f(x): Predicted Concentration", color = "black", hjust = 0) +
geom_segment(aes(x = 7.2, y = 1.6, xend = 6, yend = 0.5),
arrow = arrow(length = unit(0.2, "cm")), color = "black") +
# Adjusted annotation for Y_ij
annotate("text", x = 2, y = 4.15, label = "Yij: Observed Concentration", color = "red", hjust = 0) +
geom_segment(aes(x = 2, y = 4.1, xend = 1.1, yend = 4.15),
arrow = arrow(length = unit(0.2, "cm")), color = "red") +
# Adjusted annotation for Residual Variability
annotate("text", x = 1.8, y = 0.6, label = "Residual Unexplained Variability (σ)", color = "blue", hjust = 0.5) +
geom_segment(aes(x = 2, y = 0.8, xend = 3, yend = 1),
arrow = arrow(length = unit(0.2, "cm")), color = "blue") +
# Add a legend manually
scale_fill_manual(
name = "Components",
values = c("lightblue" = "lightblue"),
labels = c("±1σ around Prediction")
) +
guides(fill = guide_legend(override.aes = list(alpha = 0.5)))+
scale_x_continuous(breaks=seq(0,10,2))
# Display the plot
print(p)
This plot shows exemplary shows the predicted and observed concentrations as well as the residual unexplained variability around the prediction. It represents our individual or observation level of the model. This is a simple illustration; typically, datasets would not include negative concentrations and would be rather flagged as below the quantification limit.
In our case, we have only two parameters to estimate: \(\theta_{TVCL}\) and \(\omega^2\). The overall goal is to infer the parameters of interest \((\hat{\theta}_{TVCL}, \hat{\omega^2})\) from our observed data \(y_{1:n}\). In this case, \(y_{1}\) would denote the vector of \(m_i\) observations for the first individual out of n total individuals. Ideally, we would like to infer the parameters by directly maximizing the complete data log-likelihood (\(\ln L\)) function:
\[(\hat{\theta}_{TVCL}, \hat{\omega^2})_{ML} = \underset{\theta_{TVCL},~ \omega^2}{\mathrm{argmax}}~\ln L\left(\theta_{TVCL}, \omega^2| y_{1:n}, CL_{i:n}\right) \tag{3}\]
To align more with the notation in Wang (2007), we can re-write the expression based on \(\eta_i\) values instead of \(CL_i\). We can re-write:
\[(\hat{\theta}_{TVCL}, \hat{\omega^2})_{ML} = \underset{\theta_{TVCL},~ \omega^2}{\mathrm{argmax}}~\ln L\left(\theta_{TVCL}, \omega^2| y_{1:n}, \eta_{i:m}\right) \tag{4}\]
Please note that Equation 3 and Equation 4 represent the complete data log-likelihood, but more to that later in Section 5.2.2. The reason why we deal with log-likelihood is that it makes a lot of calculations a bit easier (e.g., products become sums). Furthermore, likelihood terms can become very small and this can lead to numerical difficulties. By taking the logarithm, we can avoid this issue.
Before we continue, let’s first remind ourselves what likelihood is all about and what is the difference compared to probability.
I personally see the difference between likelihood and probability as a matter of from which “direction” we are looking at the things. Probability is about looking forward (into the future): “If we have a fully specified model and set of parameters, what are the probabilities of certain future events happening?”. On the other hand, Likelihood is about looking backward: “Now that we have the data / made that particular observation, what is the most likely model or parameters that could have produced it?”
Let’s take a simple example to visualize the likelihood. We assume that the height of a human being is normally distributed and we randomly picked a guy on the streets with a height of 180 cm. Which set of parameters is more likely to lead to this height measurement? A set of parameters that assumes a mean height of 170 cm and a standard deviation of 30 cm or a set of parameters that assumes a mean height of 190 cm and a standard deviation of 5 cm?
# Define the parameter sets
params <- data.frame(
parameter_set = c("Mean = 175 cm, SD = 30 cm", "Mean = 190 cm, SD = 5 cm"),
mean = c(175, 190),
sd = c(30, 5)
)
# Define the range of heights for plotting
x_values <- seq(100, 250, by = 0.1)
# Generate density data for each parameter set
density_data <- params |>
rowwise() |>
do(data.frame(
parameter_set = .$parameter_set,
x = x_values,
density = dnorm(x_values, mean = .$mean, sd = .$sd)
)) |>
ungroup()
# Calculate the density (likelihood) at 180 cm for each parameter set
likelihoods <- params |>
rowwise() |>
mutate(density_at_180 = dnorm(180, mean = mean, sd = sd)) |>
select(parameter_set, density_at_180)
# Merge the likelihoods with the density data for plotting
density_data <- density_data |>
left_join(likelihoods, by = "parameter_set")
# Create the plot
ggplot(density_data, aes(x = x, y = density)) +
geom_line(color = "darkblue") + # Plot the density curves
facet_wrap(~ parameter_set, ncol = 1) + # Create separate panels
geom_vline(xintercept = 180, linetype = "dashed", color = "red") + # Dashed line at 180 cm
geom_point(data = likelihoods, aes(x = 180, y = density_at_180), color = "blue", size = 2, pch = 8) + # Point at 180 cm
geom_text(data = likelihoods,
aes(x = 180, y = density_at_180,
label = sprintf("Likelihood: %.5f", density_at_180)),
hjust = 1.1, vjust = -0.5, color = "blue") + # Likelihood label on the left
labs(title = "Likelihood of Observing a Height of 180 cm",
x = "Height (cm)",
y = "Density") +
theme_bw() # Apply black-and-white theme
We can see the parameters \(\mu = 175~cm\) and \(\sigma = 30~cm\) are more likely to have produced the observed height of 180 cm than the alternative set of parameters. The likelihood can be calculated with its respective probability density or probability mass function. More to that later. What becomes clear is that the concept of likelihood fundamentally requires observed data to be meaningful. And this fact leads to an issue when trying to calculate the joint likelihood for our NLME model.
We are trying to estimate the joint log-likelihood \(\ln L\left(\theta_{TVCL}, \omega^2| y_{1:n}, \eta_{i:n}\right)\), which is the likelihood of the parameters \(\theta_{TVCL}\) and \(\omega^2\) given that we have observed \(y_{1:n}\) and \(\eta_{i:n}\). Now we have a problem. While we directly observe \(y_{1:n}\), we do not observe \(\eta_i\) (or its respective \(CL_i\)) values directly. In other words: You will never receive a dataset where you have an “observed” individual clearance or an “observed” individual random effect parameter. This is why \(\eta_i\) can be called an unobserved latent variable. Previously we have defined the complete data log-likelihood in Equation 3 and Equation 4, which is the log-likelihood of both the observed data and the unobserved latent variables. But without observations for \(\eta_{i:n}\) we cannot compute the complete data likelihood.
Now what? Our approach would be to somehow get rid of the general dependence on \(\eta_i\). This is where the so-called marginal likelihood comes into play, which does not longer depend on an \(\eta_i\) observation. In our case the maximum likelihood estimates are based on the marginal likelihood:
\[(\hat{\theta}_{TVCL}, \hat{\omega^2})_{ML} = \underset{\theta_{TVCL}, \omega^2}{\mathrm{argmax}}~\ln L\left(\theta_{TVCL}, \omega^2| y_{1:n}\right) \tag{5}\]
Please note that we do not depend on an actual \(\eta_{i:n}\) observation anymore, only on \(y_{1:n}\). To set up the actual equation let’s first rewrite the Likelihood as a probability:
\[L\left(\theta_{TVCL}, \omega^2| y_{1:n}\right) = p(y_{1:n}; \theta_{TVCL}, \omega^2) \tag{6}\]
Assuming that the observations \(y_1, y_2, ..., y_n\) are independent, the likelihood can be expressed as the product of the individual likelihoods:
\[L\left(\theta_{TVCL}, \omega^2| y_{1:n}\right) = \prod_{i=1}^n p(y_{i}; \theta_{TVCL},~ \omega^2) \tag{7}\]
For each individual, we have \(m_i\) observations and \(y_{i}\) represents a vector of these \(m_i\) observations. We can also write it more explicitly to avoid misunderstandings, again assuming independence across observations.
\[L\left(\theta_{TVCL}, \omega^2| y_{1:n}\right) = \prod_{i=1}^n \prod_{j=1}^{m_i} p(y_{ij}; \theta_{TVCL},~ \omega^2) \tag{8}\]
To align the likelihood expression with the structure of our model in Equation 1 and Equation 2, we need to reformulate Equation 8 to explicitly include the individual random effects \(\eta_i\). This allows us to express the likelihood in terms of both the individual-level and population-level components, with which we can actually do calculations. In other words: Equation 8 does not yet reflect the specific hierarchical form of our model. By reformulating the likelihood (see next steps), we transform this generic form into a structure that directly incorporates our model’s individual and population components and allows us to use our previously specified model.
\[L\left(\theta_{TVCL}, \omega^2| y_{1:n}\right) = \prod_{i=1}^n \int \left( \prod_{j=1}^{m_i} p(y_{ij}, \eta_i; \theta_{TVCL}, \omega^2) \right) \cdot d\eta_i \tag{9}\]
In this first step, we are integrating over all possible values of \(\eta_i\) (since we can’t directly observe \(\eta_i\)). We can now further split this marginal likelihood equation by using the chain rule of probability, which brings us closer to the population and individual level structure of our model and closer to a state where we can use the model:
\[L\left(\theta_{TVCL}, \omega^2| y_{1:n}\right) = \prod_{i=1}^n \int \left( \prod_{j=1}^{m_i} p(y_{ij}| \eta_i; \theta_{TVCL}, \omega^2)\right) \cdot p(\eta_i | \theta_{TVCL}, \omega^2) \cdot d\eta_i \tag{10}\]
As \(p(y_{ij}| \eta_i; \theta_{TVCL}, \omega^2)\) does not actually depend on \(\omega^2\), and \(p(\eta_i | \theta_{TVCL}, \omega^2)\) does not actually depend on \(\theta_{TVCL}\), we can then simplify the equation to:
\[L\left(\theta_{TVCL}, \omega^2| y_{1:n}\right) = \prod_{i=1}^n \int \left( \prod_{j=1}^{m_i} p(y_{ij}| \eta_i; \theta_{TVCL})\right) \cdot p(\eta_i | \omega^2) \cdot d\eta_i \tag{11}\]
The integral now consists of two parts: The individual level term \(p(y_{ij}| \eta_i; \theta_{TVCL})\) and the population level term \(p(\eta_i | \omega^2)\). The intuition behind this can be seen as something like this: For a given \(\eta_i\) within the integral, the population term \(p(\eta_i |\omega^2)\) tells us how likely it is to observe this particular \(\eta_i\) value in the population. The individual term \(p(y_{ij}| \eta_i; \theta_{TVCL})\) on the other hand tells us how likely it is to observe the \(j^{th}\) observation of the \(i^{th}\) individual given that particular \(\eta_i\) value. The Likelihood will be maximal when the product of both terms is maximal, so that it is very likely to have this particular \(\eta_i\) value in the population and that it is very likely to observe the set of \(y_{ij}\) values given this \(\eta_i\) value.
So is it all good now? Kind of. We got rid of the dependence on directly observing \(\eta_i\) for the complete data log-likelihood and have instead a nice marginal likelihood equation. However, solving the marginal likelihood is much harder due to this complex integral. So the next important task is to find a way to deal with this integral. And if it is hard to calculate, why not just approximate it?
So far we’ve understood that we cannot solve the integral in the marginal likelihood equation easily. I am not sure if it is impossible or if it is just very hard to do so. But either way, in reality we need to approximate it somehow. To simplify things a bit, we will focus on the individual Likelihood \(L_i\) for now (for one single individual i) to avoid writing out the product (for the population) every time:
\[L_i\left(\theta_{TVCL}, \omega^2| y_{i}\right) = \int \left( \prod_{j=1}^{m_i} p(y_{ij}| \eta_i; \theta_{TVCL})\right) \cdot p(\eta_i | \omega^2) \cdot d\eta_i \tag{12}\]
In the end, we have to take the product of all individual Likelihoods to get the likelihood for the population. Now we are going to tackle the integral. Apparently, one way of approximating integrals is the Laplacian approximation. It is a method which simplifies difficult integrals by focusing on the most important part (contribution-wise) of the function being integrated, which is the point where the function reaches its peak (the maximum or mode of the function). The idea is to approximate the function around this maximum point by a so-called second-order Taylor expansion. This approximation assumes that the integrand behaves like a Gaussian (bell-shaped) function around its maximum. The Taylor expansion with different orders (n = 1/2/3/10) is visualized here (2024):
Now, there seems to exist an useful feature of integrals that they often become analytically solvable if they take a certain form. If we can express the integral in the following exponential form:
\[\int{\exp(f(x))~dx} \tag{13}\]
where \(f(x)\) is a second-order polynomial of the form \(f(x) = ax^2 + bx + c\) with a negative quadratic coefficient (\(a < 0\)), and \(f(x)\) is twice differentiable with a unique maximum, we can solve it analytically. Therefore, the next step would be to bring our integral into this form, so we can make use of this nice property to kick out the annoying integral. That would allow us to get rid of any integration and just directly deal with the analytical solution.
To bring our Likelihood expression into the right form, we can use a \(\exp(\ln())\) operator. In total this won’t do anything, but it allows us to simplify our inner expression a little, as products turn into sums due to the logarithm. And (as mentioned above), we need the exponential form of Equation 13 to solve the integral analytically. Thus, we take Equation 12 and apply the \(\exp(\ln())\) operator, which leads to a re-expression of the individual Likelihood as:
\[L_i\left(\theta_{TVCL}, \omega^2| y_{i}\right) = \int \exp \left(\ln \left(\left( \prod_{j=1}^{m_i} p(y_{ij}| \eta_i; \theta_{TVCL})\right)\cdot p(\eta_i | \omega^2)\right)\right) \cdot d\eta_i \tag{14}\]
After applying the log to each element, we get a sum:
\[L_i\left(\theta_{TVCL}, \omega^2| y_{i}\right) = \int \exp \left(\ln \left(\left( \prod_{j=1}^{m_i} p(y_{ij}| \eta_i; \theta_{TVCL})\right)\right) + \ln \left(p(\eta_i | \omega^2)\right)\right)\cdot d\eta_i \tag{15}\]
Also the product sum of the individual level term turns into a sum:
\[L_i\left(\theta_{TVCL}, \omega^2| y_{i}\right) = \int \exp \left( \left(\sum_{j=1}^{m_i} \ln \left(p(y_{ij}| \eta_i; \theta_{TVCL})\right)\right) + \ln \left(p(\eta_i | \omega^2)\right)\right) \cdot d\eta_i \tag{16}\]
We can now substitute the inner term with a function \(g_i(\eta_i)\), which allows us to write:
\[L_i\left(\theta_{TVCL}, \omega^2| y_{i}\right) = \int \exp\left(g_i(\eta_i)\right) \cdot d\eta_i \tag{17}\]
with
\[g_i(\eta_i) = \left(\sum_{j=1}^{m_i} \ln \left(p(y_{ij}| \eta_i; \theta_{TVCL})\right)\right) + \ln \left(p(\eta_i | \omega^2)\right) \tag{18}\]
We have successfully brought our expression into a format which allows us to later get rid of the integral itself. Please note the similarity between Equation 13 and Equation 17. In a next step we want to approximate \(g_i(\eta_i)\) as a Gaussian (second-order polynomial) function around its maximum point (mode) \(\eta_i^*\) via a Taylor expansion.
Okay, let’s approximate \(g_i(\eta_i)\) by a second order Taylor expansion of \(g_i(\eta_i)\) at point \(\eta_i^*\), as we cannot explicitly and directly calculate that integral1. A second-order Taylor expansion at point \(\eta_i^*\) is given by the following expression:
\[g_i(\eta_i) \approx g_i(\eta_i^*) + g_i'(\eta_i^*) \cdot (\eta_i - \eta_i^*) + \frac{1}{2} g_i''(\eta_i^*)(\eta_i-\eta_i^*)^2 \tag{19}\]
During Laplacian estimation, we want to choose \(\eta_i^*\) so that we are in the mode of \(g_i\). First of all, around this point we have the biggest contribution to the integral. Since a Taylor approximation is always most accurate at the point for which we are expanding it, it makes sense that this should be the point at which the integral is the most sensitive to. Second, the mode is the point where the first derivative (\(g_i'(\eta_i^*)\)) is zero. Therefore, it allows us to drop the second term of the Taylor expansion:
\[g_i(\eta_i) \approx g_i(\eta_i^*) + \frac{1}{2} g_i''(\eta_i^*)(\eta_i-\eta_i^*)^2 \tag{20}\]
given that
\[\eta_i^* = \underset{\eta_i}{\mathrm{argmax}}\left[g_i(\eta_i)\right] = \underset{\eta_i}{\mathrm{argmax}}\left[\left(\sum_{j=1}^{m_i} \ln \left(p(y_{ij}| \eta_i; \theta_{TVCL})\right)\right) + \ln \left(p(\eta_i | \omega^2)\right)\right] \tag{21}\]
Great! Now we have approximated the complex expression \(g_i(\eta_i)\) and can now try to get rid of the integral in a next step.
Okay, so the first thing we do is to take Equation 17 and substitute \(g_i(\eta_i)\) with the 2nd-order approximation we obtained via Equation 20. This gives us:
\[L_i\left(\theta_{TVCL}, \omega^2| y_{i}\right) = \int \exp\left(g_i(\eta_i^*) + \frac{1}{2} g_i''(\eta_i^*)(\eta_i-\eta_i^*)^2\right) \cdot d\eta_i \tag{22}\]
Our first goal is to isolate expressions which are dependent on \(\eta_i\) and those which are not. This will later allow us to get rid of the integral. The term \(g_i(\eta_i^*)\) is independent on \(\eta_i\) (it is just being evaluated at the mode \(\eta_i^*\)), while the term \(\frac{1}{2} g_i''(\eta_i^*)(\eta_i-\eta_i^*)^2\) is actually dependent on \(\eta_i\). Therefore, we are now going to split the expression into two parts:
\[L_i\left(\theta_{TVCL}, \omega^2| y_{i}\right) = \int \exp\left(g_i(\eta_i^*)\right) \cdot \exp\left( \frac{1}{2} g_i''(\eta_i^*)(\eta_i-\eta_i^*)^2\right) \cdot d\eta_i \tag{23}\]
Now in order that our plan (kicking out the integral) works, we need to ensure that the exponent of the second term is negative. This is important, because we want to approximate the integral as a Gaussian function, which is only possible if this exponent is negative. Technically, we can be sure that this is the case, because we are expanding around the mode and the second derivative at this point is negative for our function. However, since I want to align more with the reference solution in Wang (2007), I re-write the expression in a way that makes this more explicit:
\[L_i\left(\theta_{TVCL}, \omega^2| y_{i}\right) = \int \exp\left(g_i(\eta_i^*)\right) \cdot \exp\left( -\frac{1}{2} \left| g_i''(\eta_i^*)\right| (\eta_i-\eta_i^*)^2\right) \cdot d\eta_i \tag{24}\]
We just introduced a negative sign and took the absolute value of the second derivative. Now we can substitute \(g_i(\eta_i^*)\) with the respective expression given in Equation 18 (and evaluated at the mode \(\eta_i^*\)) and get:
\[\begin{split} L_i\left(\theta_{TVCL}, \omega^2| y_{i}\right) = \int \exp\left(\left(\sum_{j=1}^{m_i} \ln \left(p(y_{ij}| \eta_i^*; \theta_{TVCL})\right)\right) + \ln \left(p(\eta_i^* | \omega^2)\right)\right) \\ \cdot \exp\left( -\frac{1}{2} \left| g_i''(\eta_i^*)\right| (\eta_i-\eta_i^*)^2\right) \cdot d\eta_i \end{split} \tag{25}\]
Now the term \(\exp\left(\left(\sum_{j=1}^{m_i} \ln \left(p(y_{ij}| \eta_i^*; \theta_{TVCL})\right)\right) + \ln \left(p(\eta_i^* | \omega^2)\right)\right)\) does not depend anymore on \(\eta_i\) (over which we are integrating), since the expression is just evaluated at a given value of \(\eta_i^*\). This means it is a constant and can be factored out of the integral:
\[ \begin{split} L_i\left(\theta_{TVCL}, \omega^2| y_{i}\right) = \exp\left(\left(\sum_{j=1}^{m_i} \ln \left(p(y_{ij}| \eta_i^*; \theta_{TVCL})\right)\right) + \ln \left(p(\eta_i^* | \omega^2)\right)\right) \\ \cdot\int \exp\left( -\frac{1}{2} \left| g_i''(\eta_i^*)\right| (\eta_i-\eta_i^*)^2\right) \cdot d\eta_i \end{split} \tag{26}\]
Remember the trick we have used to bring the integral in the right form? This operator \(\exp(\ln())\) is not needed for the term which has been factored out, so we can simplify it to \(\left(\prod_{j=1}^{m_i} p(y_{ij}| \eta_i^*; \theta_{TVCL})\right) \cdot p(\eta_i^* | \omega^2)\). Please note, that the summation becomes a product again as we transform to the normal domain:
\[L_i\left(\theta_{TVCL}, \omega^2| y_{i}\right) = \left(\prod_{j=1}^{m_i} p(y_{ij}| \eta_i^*; \theta_{TVCL})\right) \cdot p(\eta_i^* | \omega^2) \cdot \int \exp\left( -\frac{1}{2} \left| g_i''(\eta_i^*)\right| (\eta_i-\eta_i^*)^2\right) \cdot d\eta_i \tag{27}\]
Now the whole plan of those people, who came up with this derivation, works out: The remaining integral is the integral of a Gaussian function and can be solved analytically. We now shortly just focus on the integral part of Equation 27:
\[\int \exp\left( -\frac{1}{2} \left| g_i''(\eta_i^*)\right| (\eta_i-\eta_i^*)^2\right) \cdot d\eta_i \tag{28}\]
In general, a Gaussian integral has the following form (and analytical solution):
\[\int \exp\left(-\frac{1}{2} \frac{x^2}{\sigma^2} \right) dx = \sqrt{2\pi\sigma^2} \tag{29}\]
To see how our expression fits this form, we notice that
\[-\frac{1}{2} \left| g_i''(\eta_i^*)\right| (\eta_i-\eta_i^*)^2 \tag{30}\]
can be written as \(-\frac{1}{2} x^2\) via the substitution
\[x = \sqrt{\left| g_i''(\eta_i^*)\right|} (\eta_i-\eta_i^*), ~~ d\eta_i = \frac{1}{\sqrt{\left| g_i''(\eta_i^*)\right|}} \cdot dx \tag{31}\]
Hence, we obtain:
\[\int \exp\left(-\frac{1}{2} \left| g_i''(\eta_i^*)\right| (\eta_i-\eta_i^*)^2 \right) \cdot d\eta_i = \int \exp\left(-\frac{1}{2} x^2\right) \cdot \frac{1}{\sqrt{\left| g_i''(\eta_i^*)\right|}} dx \tag{32}\]
which evaluates to
\[\frac{1}{\sqrt{\left| g_i''(\eta_i^*)\right|}} \cdot \sqrt{2 \pi} = \sqrt{2 \pi \cdot \frac{1}{\left| g_i''(\eta_i^*)\right|}} = \sqrt{\frac{2\pi}{\left| g_i''(\eta_i^*)\right|}} \tag{33}\]
Finally the magic happens. With all the work we have invested we can finally harvest the fruits. The integral disappears and we are left with a simple expression.
\[\int \exp\left( -\frac{1}{2} \left| g_i''(\eta_i^*)\right| (\eta_i-\eta_i^*)^2\right) \cdot d\eta_i = \sqrt{2\pi\cdot \frac{1}{\left| g_i''(\eta_i^*)\right|} } = \sqrt{\frac{2\pi}{\left| g_i''(\eta_i^*)\right|}} \tag{34}\]
To my understanding we have now achieved an important goal by turning a hard-to calculate integral into an analytical expression, which is easier to evaluate. The only challenge remaining is the calculation of the second derivative \(g_i''(\eta_i^*)\), which is not very straightforward. Substituting the simplified integral part from Equation 34 back into our individual likelihood expression (Equation 27), we get:
\[L_i\left(\theta_{TVCL}, \omega^2| y_{i}\right) = \left(\prod_{j=1}^{m_i} p(y_{ij}| \eta_i^*; \theta_{TVCL})\right) \cdot p(\eta_i^*|\omega^2) \cdot \sqrt{\frac{2\pi}{\left| g_i''(\eta_i^*)\right|}} \tag{35}\]
Also here, we need to be careful. As mentioned above, \(g_i''(\eta_i^*)\) is expected to be negative, since the function is concave and has a negative curvature at their maximum. I saw in Wang (2007) that they write \(-g_i''(\eta_i^*)\), however, this should be the same as \(|g_i''(\eta_i^*)|\) and I am going to stick to the absolute value out of convenience and because I find it a bit easier to follow.
Now we can move a step further and translate it into something which is more familiar to us: The objective function in NONMEM. In the next section, we are going to spell out the missing expressions and also define the actual equation for the second derivative \(g_i''(\eta_i^*)\).
Okay, so our next task is to define the objective function in NONMEM. We know that NONMEM calculates the -2 log likelihood (Bauer 2020). To my understanding the main reason to use the log of the Likelihood is to make it numerically more stable and the main reason to take the -2 is to make it asymptotically chi-square distributed (and thus, it allows some statistical testing). The negative sign turns our maximization problem into a minimization problem, which is mathematically easier to solve. The -2 log likelihood for a single individual is defined as:
\[OF_i = -2\ln L_i\left(\theta_{TVCL}, \omega^2| y_{i}\right) \tag{36}\]
For the sake of simplicity we are still focusing on a single individual \(i\) and its contribution to the objective function. In the end, we would have to sum up the individual contributions to the objective function \(OF_i\) to get the final objective function. When we substitute the individual likelihood from Equation 35 into Equation 36, we get:
\[OF_i = -2\ln\left(\left(\prod_{j=1}^{m_i} p(y_{ij}| \eta_i^*; \theta_{TVCL})\right) \cdot p(\eta_i^*|\omega^2) \cdot \sqrt{\frac{2\pi}{\left| g_i''(\eta_i^*)\right|}}\right) \tag{37}\]
We can apply the \(-2\ln()\) operation to each element and are left with:
\[OF_i = -2 \ln \left(\prod_{j=1}^{m_i} p(y_{ij}| \eta_i^*; \theta_{TVCL})\right) -2 \ln \left(p(\eta_i^*|\omega^2)\right) -2 \ln \left(\sqrt{\frac{2\pi}{\left| g_i''(\eta_i^*)\right|}}\right) \tag{38}\]
This can be re-written as:
\[OF_i = \left(\sum_{j=1}^{m_i} -2 \ln\left(p(y_{ij}| \eta_i^*; \theta_{TVCL})\right)\right) -2 \ln \left(p(\eta_i^*|\omega^2)\right) -2 \ln \left(\sqrt{\frac{2\pi}{\left| g_i''(\eta_i^*)\right|}}\right) \tag{39}\]
From here on it makes sense to split up the terms in order to better understand what is going on. We can identify three terms in the expression given by Equation 39:
Let’s spell out each of these terms in more detail and see how they can be calculated.
Let’s tackle the first term of Equation 39. It is given by:
\[\left(\sum_{j=1}^{m_i} -2 \ln\left(p(y_{ij}| \eta_i^*; \theta_{TVCL})\right)\right) \tag{40}\]
The question we are asking is: “How likely is it to observe a certain set of data points \(y_i\) (= a series of observations for an individual) given the individual (most likely) parameter \(\eta_i^*\) and \(\theta_{TVCL}\)?” Please note: It seems that this expression is independent of \(\omega^2\), but it is not. Our most likely \(\eta_i^*\) is the mode of the distribution characterized by \(\omega^2\), so we have a hidden dependence here. Typically, the our first term would also involve the residual unexplained variance (RUV) given by \(\sigma^2\), but in our simple example it is fixed to a certain variance and thus, we don’t have to estimate it.
We assume a normal distribution (given by the RUV) around our model predictions \(f(x_{ij}; \theta_i)\). Please refer to Figure 7 for a refresher. Now we can illustrate this concept for one single data point of a single individual (e.g., after 10 h a concentration of 2 mg/L was measured) as a case example to understand the concept a bit better:
# Set seed for reproducibility (optional)
set.seed(123)
# Define fixed parameters
Dose <- 100 # Dose administered
V_D <- 10 # Volume of distribution
eta_i <- 0 # Individual random effect
sigma <- sqrt(0.1) # Residual unexplained variance (standard deviation)
# Define population parameters (Theta_TVCL)
Theta_TVCL_values <- c(10, 15, 20)
# Define fixed time point (t)
t <- 1 # You can change this as needed
# Compute the structural model predictions for each Theta_TVCL
# Using the formula: C(t) = (Dose / V_D) * exp(-Theta_TVCL / V_D * t)
model_predictions <- data.frame(
Theta_TVCL = Theta_TVCL_values,
C_t = (Dose / V_D) * exp(-Theta_TVCL_values / V_D * t)
)
# Define the observed data point y_i
y_i <- 2
# Create a sequence of y values for plotting the PDFs
y_values <- seq(min(model_predictions$C_t) - 3*sigma,
max(model_predictions$C_t) + 3*sigma,
length.out = 1000)
# Create a data frame with density values for each Theta_TVCL
density_data <- model_predictions |>
rowwise() |>
do(data.frame(
Theta_TVCL = .$Theta_TVCL,
y = y_values,
density = dnorm(y_values, mean = .$C_t, sd = sigma)
)) |>
ungroup()
# Calculate the likelihood and -2 log likelihood for the observed y_i
likelihood_data <- model_predictions |>
mutate(
likelihood = dnorm(y_i, mean = C_t, sd = sigma),
neg2_log_likelihood = -2 * log(likelihood)
)
# Merge likelihood data with density_data for annotation purposes
density_data <- density_data |>
left_join(likelihood_data, by = "Theta_TVCL")
# Create a named vector for custom facet labels
facet_labels <- setNames(
paste("TVCL =", Theta_TVCL_values),
Theta_TVCL_values
)
# Start plotting
ggplot(density_data, aes(x = y, y = density)) +
# Plot the density curves
geom_line(color = "blue", size = 1) +
# Add a vertical line for the observed data point y_i
geom_vline(xintercept = y_i, linetype = "dashed", color = "red") +
# Facet the plot by Theta_TVCL
facet_wrap(~ Theta_TVCL, scales = "free_y", labeller = as_labeller(facet_labels), nrow=3) +
# Add annotations for the likelihood and -2 log likelihood
geom_text(data = density_data |> distinct(Theta_TVCL, likelihood, neg2_log_likelihood),
aes(x = Inf, y = Inf,
label = paste0("Likelihood: ", round(likelihood, 6),
"\n-2 ln(L): ", round(neg2_log_likelihood, 3))),
hjust = 1.1, vjust = 1.1, size = 4, color = "black") +
# Customize labels and theme
labs(
title = "Likelihood for different TVCL values",
subtitle = paste("Observed data point yi =", y_i, ", eta_i* = 0"),
x = "Concentration (C(t))",
y = "Probability Density"
) +
theme_bw() +
scale_y_continuous(limits=c(NA, 2))+
theme(
strip.text = element_text(size = 12, face = "bold"),
plot.title = element_text(size = 14, face = "bold"),
plot.subtitle = element_text(size = 12)
)
For simplicity we have assumed an \(\eta_i^*\) of 0 to generate this plot. We can see that we have observed a concentration of 2 mg/L at a given time point and want to know how likely it is to observe this particular concentration given different values of \(\theta_{TVCL}\) with a fixed \(\eta_i^*\). It becomes apparent that it is much more likely to have a clearance of 15 L/h given our data than to have a clearance of 10 or 20 L/h. But how can we explicitly calculate that likelihood given by Equation 40?
Since we deal with a normal distribution, the likelihood is given by its probability density function (PDF). The general form is given by:
\[pdf(\text{obs}) = \frac{1}{\sqrt{2\pi \sigma^2}}\, \exp\left(-\frac{(\text{obs} - \mu)^2}{2\sigma^2}\right) \tag{41}\]
In our case we would re-write it as follows for a single observation \(y_{ij}\):
\[p(y_{ij} | \eta_i^*; \theta_{TVCL}) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left(-\frac{(y_{ij} - f(x_{ij}, \theta_{TVCL}, \eta_i^*))^2}{2\sigma^2}\right) \tag{42}\]
Taking the log leads to:
\[\ln \left(p(y_{ij} | \eta_i^*; \theta_{TVCL})\right) = -\frac{1}{2} \ln(2\pi\sigma^2) - \frac{(y_{ij} - f(x_{ij}, \theta_{TVCL}, \eta_i^*))^2}{2\sigma^2} \tag{43}\]
Multiplying with -2 and simplifying leads to:
\[-2 \ln \left(p(y_{ij} | \eta_i^*; \theta_{TVCL})\right) = \ln(2\pi\sigma^2) + \frac{(y_{ij} - f(x_{ij}, \theta_{TVCL}, \eta_i^*))^2}{\sigma^2} \tag{44}\]
In a last step, we would have to take the sum of all observations to consider the likelihood contributions of all datapoints:
\[\left(\sum_{j=1}^{m_i} -2 \ln\left(p(y_{ij}| \eta_i^*; \theta_{TVCL})\right)\right) = \sum_{j=1}^{m_i} \left[\ln(2\pi\sigma^2) + \frac{(y_{ij} - f(x_{ij}, \theta_{TVCL}, \eta_i^*))^2}{\sigma^2}\right] \tag{45}\]
Great! If someone would give us a \(\theta_{TVCL}\) value and an \(\eta_i^*\) value, we would be able to calculate the -2 log likelihood term for that particular data point. Actually, we would need to have the model prediction function at hand for this (or an ODE-solver). The model prediction \(f(x_{ij}, \theta_{TVCL}, \eta_i^*)\) was already defined in Equation 69 (see above). It will be used at various points of the final objective function.
A very similar concept applies to the second term of Equation 39. It is given by:
\[-2 \ln \left(p(\eta_i^*|\omega^2)\right) \tag{46}\]
We typically assume that \(\eta_i\) is normally distributed with a mean of 0 with a variance \(\omega^2\). We could do a similar illustration as above, where we have a look at a certain \(\eta_i^*\) value and want to know how likely it is to observe this value given the population variance \(\omega^2\) (which we have at the moment of evaluation):
# Set seed for reproducibility (optional)
set.seed(123)
# Define fixed parameters
eta_i_star <- 0.3 # Observed eta_i value
omega_squared_values <- c(0.01, 0.2, 0.5) # Population variances
# Define the mean for eta_i (assumed to be 0)
mu_eta <- 0
# Compute the structural model predictions for each omega^2
# Using the formula: eta_i ~ N(0, omega^2)
model_predictions <- data.frame(
omega_squared = omega_squared_values,
mean = mu_eta
)
# Create a sequence of eta values for plotting the PDFs
# Extending the range to cover the tails adequately
eta_values <- seq(
mu_eta - 4 * sqrt(max(omega_squared_values)),
mu_eta + 4 * sqrt(max(omega_squared_values)),
length.out = 1000
)
# Create a data frame with density values for each omega^2
density_data <- model_predictions |>
rowwise() |>
do(data.frame(
omega_squared = .$omega_squared,
eta = eta_values,
density = dnorm(eta_values, mean = .$mean, sd = sqrt(.$omega_squared))
)) |>
ungroup()
# Calculate the likelihood and -2 log likelihood for the observed eta_i*
likelihood_data <- model_predictions |>
mutate(
likelihood = dnorm(eta_i_star, mean = mean, sd = sqrt(omega_squared)),
neg2_log_likelihood = -2 * log(likelihood)
)
# Merge likelihood data with density_data for annotation purposes
density_data <- density_data |>
left_join(likelihood_data, by = "omega_squared")
# Create a named vector for custom facet labels
facet_labels <- setNames(
paste("ω² =", omega_squared_values),
omega_squared_values
)
# Start plotting
ggplot(density_data, aes(x = eta, y = density)) +
# Plot the density curves
geom_line(color = "blue", size = 1) +
# Add a vertical line for the observed eta_i*
geom_vline(xintercept = eta_i_star, linetype = "dashed", color = "red") +
# Highlight the point (eta_i*, density at eta_i*)
geom_point(
data = density_data |> filter(abs(eta - eta_i_star) < 1e-6),
aes(x = eta, y = density),
color = "darkgreen", size = 3
) +
# Facet the plot by omega_squared with custom labels
facet_wrap(
~ omega_squared,
scales = "free_y",
labeller = as_labeller(facet_labels),
nrow=3
) +
# Add annotations for the likelihood and -2 log likelihood
geom_text(
data = likelihood_data,
aes(
x = Inf, y = Inf,
label = paste0(
"Likelihood: ", round(likelihood, 4),
"\n-2 log(L): ", round(neg2_log_likelihood, 2)
)
),
hjust = 1.1, vjust = 1.1, size = 4, color = "black"
) +
# Customize labels and theme
labs(
title = "Likelihood term for different ω² values",
subtitle = paste("etai* =", eta_i_star),
x = expression(eta),
y = "Probability Density"
) +
theme_bw() +
scale_y_continuous(limits=c(NA, 4.5))+
theme(
strip.text = element_text(size = 12, face = "bold"),
plot.title = element_text(size = 14, face = "bold"),
plot.subtitle = element_text(size = 12)
)
In our little example we can observe that the likelihood of “observing”2 \(\eta_i^* = 0.3\) is much higher when the IIV variance is 0.2 compared to 0.01 or 0.5. This is the information we want to capture with this second likelihood term. Similarly to the first term of Equation 39, we are applying the general form of the pdf (Equation 41), which leads to this expression:
\[p(\eta_i^*|\omega^2) = \frac{1}{\sqrt{2\pi\omega^2}} \exp\left(-\frac{(\eta_i^* - 0)^2}{2\omega^2}\right) \tag{47}\]
Please note that the normal distribution is centered around 0 (\(\mu = 0\)), which is in contrast to the individual level where it was centered around the predicted value \(f(x_{ij}, \theta_{TVCL}, \eta_i^*)\) (see Equation 42). Because of \(\mu = 0\), we can simplify this to:
\[p(\eta_i^*|\omega^2) = \frac{1}{\sqrt{2\pi\omega^2}} \exp\left(-\frac{\eta_i^{*2}}{2\omega^2}\right) \tag{48}\]
Taking the log:
\[\ln \left(p(\eta_i^*|\omega^2)\right) = -\frac{1}{2} \ln(2\pi\omega^2) - \frac{\eta_i^{*2}}{2\omega^2} \tag{49}\]
Multiplying with -2 and simplifying:
\[-2 \ln \left(p(\eta_i^*|\omega^2)\right) = \ln(2\pi\omega^2) + \frac{\eta_i^{*2}}{\omega^2} \tag{50}\]
Very good. We have our population-level likelihood term. Similar to Term 1, we are now able to calculate this expression if someone would give us a value for \(\eta_i^*\) and \(\omega^2\). The remaining term is part 3 of the objective function, which is a bit more tricky. Let’s move on to this term.
The derivative term is the third and last term of Equation 39 and is given by
\[-2 \ln \left(\sqrt{\frac{2\pi}{\left| g_i''(\eta_i^*)\right|}}\right) \tag{51}\]
We can take the square root out of the logarithm:
\[-2 \ln \left(\sqrt{\frac{2\pi}{\left| g_i''(\eta_i^*)\right|}}\right) = -2 \cdot \frac{1}{2} \cdot \ln \left(\frac{2\pi}{\left| g_i''(\eta_i^*)\right|}\right) \tag{52}\]
Which can be simplified to:
\[-2 \ln \left(\sqrt{\frac{2\pi}{\left| g_i''(\eta_i^*)\right|}}\right) = - \ln \left(\frac{2\pi}{\left| g_i''(\eta_i^*)\right|}\right) \tag{53}\]
This expression can be further simplified by applying log-rules to:
\[-2 \ln \left(\sqrt{\frac{2\pi}{\left| g_i''(\eta_i^*)\right|}}\right) = - \ln \left(2\pi\right) + \ln\left(\left|g_i''(\eta_i^*)\right|\right) \tag{54}\]
We still need to find a way to calculate the second derivative of the individual model function \(g_i(\eta_i^*)\). However, defining the second derivative \(g_i''(\eta_i^*)\) evaluated at \(\eta_i^*\) is not straightforward and in many cases (once we deal with more complex models), this would be approximated numerically (e.g., using finite difference methods). We have luckily chosen a very simple model and can actually calculate the second derivative of the closed form expression. However, it is still quite complicated and cumbersome (at least to me). Therefore, we will simply use WolframAlpha / Mathematica to find these derivatives and help us out with the derivation rules.
The function \(g_i(\eta_i)\) was already defined in Equation 18. Given that, the second derivative is expressed as the second derivatives of its two terms:
\[g_i''(\eta_i^*) = \left[\left(\sum_{j=1}^{m_i} \ln \left(p(y_{ij}| \eta_i^*; \theta_{TVCL})\right)\right)\right]'' + \left[ln\left(p(\eta_i^*|\omega^2)\right)\right]'' \tag{55}\]
We will use WolframAlpha to calculate the second derivative for both parts.
Let’s start with the first part, which is given by:
\[\left[\left(\sum_{j=1}^{m_i} \ln \left(p(y_{ij}| \eta_i^*; \theta_{TVCL})\right)\right)\right]'' \tag{56}\]
It doesn’t matter whether we differentiate each term of a sum individually and then add the results, or add the terms first and then differentiate the sum as a whole. The result remain the same due to the linearity property of differentiation. For this reason, we first define the second derivative of a single term (by ignoring the sum). Our expression for \(\ln \left(p(y_{ij}| \eta_i^*; \theta_{TVCL})\right)\) is given in Equation 43.
According to WolframAlpha, the second derivative of Equation 43 is given by:
\[\begin{multline} \left[\ln \left(p(y_{ij}| \eta_i^*; \theta_{TVCL})\right)\right]'' = \\ \frac{-(f'(x_{ij}, \theta_{TVCL}, \eta_i^*))^2 + \left(y_{ij} - f(x_{ij}, \theta_{TVCL}, \eta_i^*)\right) \cdot f''(x_{ij}, \theta_{TVCL}, \eta_i^*)}{\sigma^2} \end{multline} \tag{57}\]
Subsequently, we have to take the sum of these derivatives over all \(j\) (see above):
\[\begin{multline} \left[\left(\sum_{j=1}^{m_i} \ln \left(p(y_{ij}| \eta_i; \theta_{TVCL})\right)\right)\right]'' = \\ \sum_{j=1}^{m_i} \left[ \frac{-(f'(x_{ij}, \theta_{TVCL}, \eta_i^*))^2 + \left(y_{ij} - f(x_{ij}, \theta_{TVCL}, \eta_i^*)\right) \cdot f''(x_{ij}, \theta_{TVCL}, \eta_i^*)}{\sigma^2} \right] \end{multline} \tag{58}\]
The closed form expression for the model prediction function is defined in Equation 69. However, we haven’t defined its first and second derivative yet. Similar, we are going to use WolframAlpha to define these derivatives:
\[f'(x_{ij}, \theta_{TVCL}, \eta_i^*) = -\frac{\theta_{TVCL} \cdot t_{ij} \cdot e^{\eta_i^*}}{V_D} \cdot f(x_{ij}, \theta_{TVCL}, \eta_i^*) \tag{59}\]
\[f''(x_{ij}, \theta_{TVCL}, \eta_i^*) = \frac{\theta_{TVCL} \cdot t_{ij} \cdot e^{\eta_i^*}}{V_D} \cdot \left( \frac{\theta_{TVCL} \cdot t_{ij} \cdot e^{\eta_i^*}}{V_D} -1\right) \cdot f(x_{ij}, \theta_{TVCL}, \eta_i^*) \tag{60}\]
This provides us with everything we need for the first part of term 3.
The second part of the second derivative is given by:
\[\left[ln\left(p(\eta_i^*|\omega^2)\right)\right]'' \tag{61}\]
Its full expression is given by Equation 49 and the second derivative is defined as:
\[\left[ln\left(p(\eta_i^*|\omega^2)\right)\right]'' = - \frac{1}{\omega^2} \tag{62}\]
Now we can substitute the terms in Equation 55 to get the full expression for \(\left[g_i(\eta_i^*)\right]''\):
\[\begin{multline} \left[g_i(\eta_i^*)\right]'' = \\ \sum_{j=1}^{m_i} \left[ \frac{-(f'(x_{ij}, \theta_{TVCL}, \eta_i^*))^2 + \left(y_{ij} - f(x_{ij}, \theta_{TVCL}, \eta_i^*)\right) \cdot f''(x_{ij}, \theta_{TVCL}, \eta_i^*)}{\sigma^2} \right] - \frac{1}{\omega^2} \end{multline} \tag{63}\]
which depends on our previous definitions for \(f'(x_{ij}, \theta_{TVCL}, \eta_i^*)\) in Equation 59 and \(f''(x_{ij}, \theta_{TVCL}, \eta_i^*)\) in Equation 60.
Now we have to pluck our results back into Equation 54 to finalize term 3:
\[\begin{multline} -2 \ln \left(\sqrt{\frac{2\pi}{\left| g_i''(\eta_i^*)\right|}}\right) = - \ln \left(2\pi\right) + \\ \ln\left(\left| \sum_{j=1}^{m_i} \left[ \frac{-(f'(x_{ij}, \theta_{TVCL}, \eta_i^*))^2 + \left(y_{ij} - f(x_{ij}, \theta_{TVCL}, \eta_i^*)\right) \cdot f''(x_{ij}, \theta_{TVCL}, \eta_i^*)}{\sigma^2} \right] - \frac{1}{\omega^2} \right|\right) \end{multline} \tag{64}\]
Great! We have found the final expression for the second derivative of \(g_i(\eta_i^*)\).
Our first task is to find the particular value of \(\eta_i\) which maximizes the expression in Equation 18. This should be nothing else than a Bayesian maximum a-posteriori (MAP) estimation (or empirical Bayes estimation (EBE)). We can find the mode of \(g_i(\eta_i)\) by:
\[\eta_i^* = \underset{\eta_i}{\mathrm{argmax}}g_i(\eta_i) = \underset{\eta_i}{\mathrm{argmax}}\left[\left(\sum_{j=1}^{m_i} \ln \left(p(y_{ij}| \eta_i; \theta_{TVCL})\right)\right) + \ln \left(p(\eta_i | \omega^2)\right)\right] \tag{65}\]
This means that we are searching over all possible values for \(\eta_i\) (per individual) and try to find the value that maximizes our log likelihood function. We have already previously defined \(\ln\left(p(y_{ij} | \eta_i; \theta_{TVCL})\right)\) and \(ln\left(p(\eta_i|\omega^2)\right)\) in Equation 43 and Equation 49, respectively3. We can substitute these expressions into Equation 65:
\[\eta_i^* = \underset{\eta_i}{\mathrm{argmax}} ~\left[\sum_{j=1}^{m_i} \left[-\frac{1}{2} \ln(2\pi\sigma^2) - \frac{(y_{ij} - f(x_{ij}, \theta_{TVCL}, \eta_i))^2}{2\sigma^2}\right] -\frac{1}{2} \ln(2\pi\omega^2) - \frac{\eta_i^{2}}{2\omega^2}\right] \tag{66}\]
Now this is an optimization (maximization) problem, so we don’t care about the constants. This simplifies the expression to:
\[\eta_i^* = \underset{\eta_i}{\mathrm{argmax}} ~\left[\sum_{j=1}^{m_i} \left[ - \frac{(y_{ij} - f(x_{ij}, \theta_{TVCL}, \eta_i))^2}{2\sigma^2}\right] - \frac{\eta_i^{2}}{2\omega^2}\right] \tag{67}\]
Most numerical optimization algorithms are designed to minimize functions, because it is conceptually simpler to identify a minimum than a maximum. As we will later reproduce this function in R, we are already now turning the maximization problem into a minimization problem by negation:
\[\eta_i^* = \underset{\eta_i}{\mathrm{argmin}} ~\left[\sum_{j=1}^{m_i} \left[\frac{(y_{ij} - f(x_{ij}, \theta_{TVCL}, \eta_i))^2}{2\sigma^2}\right] + \frac{\eta_i^{2}}{2\omega^2}\right] \tag{68}\]
In our simple example, we luckily do not need to rely on ODE solvers (as we have an analytical solution at hand) and can later replace \(f(x_{ij}, \theta_{TVCL}, \eta_i)\) with the closed form expression of a 1 cmt iv bolus model:
\[f(x_{ij}, \theta_{TVCL}, \eta_i) = \frac{Dose}{V_D} \cdot \exp(-\frac{\theta_{TVCL} \cdot e^{\eta_{i}}}{V_D}t_{ij}) \tag{69}\]
Equation 68 needs to be numerically optimized for each individual at each iteration of the algorithm. This is typically done by using a numerical optimization algorithm. The optimization algorithm will search the parameter space to numerically find the value of \(\eta_i^*\) that maximizes the function.
Previously, we have taken the three pieces of Equation 39 and expressed them in an explicit way. Let’s put them together. After simplification, our objective function is represented by:
\[OF_i = a + b + c \tag{70}\]
where \(a\), \(b\), and \(c\) are defined based on Equation 45, Equation 50, and Equation 64:
\[a = \sum_{j=1}^{m_i} \left[\ln(2\pi\sigma^2) + \frac{(y_{ij} - f(x_{ij}, \theta_{TVCL}, \eta_i^*))^2}{\sigma^2}\right] \tag{71}\]
\[b = \ln(2\pi\omega^2) + \frac{\eta_i^{*2}}{\omega^2} \tag{72}\]
\[\begin{multline} c = - \ln \left(2\pi\right) + \\ \ln\left(\left| \sum_{j=1}^{m_i} \left[ \frac{-(f'(x_{ij}, \theta_{TVCL}, \eta_i^*))^2 + \left(y_{ij} - f(x_{ij}, \theta_{TVCL}, \eta_i^*)\right) \cdot f''(x_{ij}, \theta_{TVCL}, \eta_i^*)}{\sigma^2} \right] - \frac{1}{\omega^2} \right|\right) \end{multline} \tag{73}\]
leading to
\[\begin{multline} OF_i = \sum_{j=1}^{m_i} \left[\ln(2\pi\sigma^2) + \frac{(y_{ij} - f(x_{ij}, \theta_{TVCL}, \eta_i^*))^2}{\sigma^2}\right] + \ln(2\pi\omega^2) + \frac{\eta_i^{*2}}{\omega^2} - \ln \left(2\pi\right) + \\ \ln\left(\left| \sum_{j=1}^{m_i} \left[ \frac{-(f'(x_{ij}, \theta_{TVCL}, \eta_i^*))^2 + \left(y_{ij} - f(x_{ij}, \theta_{TVCL}, \eta_i^*)\right) \cdot f''(x_{ij}, \theta_{TVCL}, \eta_i^*)}{\sigma^2} \right] - \frac{1}{\omega^2} \right|\right) \end{multline} \tag{74}\]
It seems that NONMEM ignores all constants during the optimization process (Bauer (2020) and Wang (2007)), which is why we can get rid of the \(\ln(2\pi)\) terms. We can simplify to:
\[\begin{multline} OF_i = \sum_{j=1}^{m_i} \left[\ln(\sigma^2) + \frac{(y_{ij} - f(x_{ij}, \theta_{TVCL}, \eta_i^*))^2}{\sigma^2}\right] + \ln(\omega^2) + \frac{\eta_i^{*2}}{\omega^2} + \\ \ln\left(\left| \sum_{j=1}^{m_i} \left[ \frac{-(f'(x_{ij}, \theta_{TVCL}, \eta_i^*))^2 + \left(y_{ij} - f(x_{ij}, \theta_{TVCL}, \eta_i^*)\right) \cdot f''(x_{ij}, \theta_{TVCL}, \eta_i^*)}{\sigma^2} \right] - \frac{1}{\omega^2} \right|\right) \end{multline} \tag{75}\]
Please note that the objective function \(OF_i\) is a function with multiple input parameters. Technically, we would have to write something like this:
\[OF_i\left(\theta_{TVCL}, \omega^2, \sigma^2, y_i, \eta_i^*, x_i = \left[DOSE_i, V_D, t_i\right]\right) = (...)\]
to clearly state the dependencies. However, for the sake of readability we are simply denoting it \(OF_i\). The last step would be now to calculate the objective function for the whole population, including n individuals:
\[OF = \sum_{i=1}^{n} OF_i \tag{76}\]
Very good. We have now set up the final equation for our objective function and we can now reproduce these function in R!
In order to reproduce the iteration of the NONMEM algorithm, we need to define a couple of functions inside R. Technically, we need all equations which are part of Equation 75. In the next steps we are going to define these functions in R.
The first function we are defining in R is Equation 69, which gives us a prediction for a given \(x_{ij}, \theta_{TVCL}, \eta_i\) based on our structural model.
function: f_pred()
# Define structural model prediction function
f_pred <- function(eta_i, dose, vd, theta_tvcl, t) {
exp_eta_i <- exp(eta_i)
exponent <- -1 * (theta_tvcl * exp_eta_i / vd) * t
result <- (dose / vd) * exp(exponent)
return(result)
}We also have to define the derivatives of f_pred(). This is the definition of the first derivative function (reproduction of Equation 59):
function: f_prime()
# Define the first derivative of the structural model prediction function
f_prime <- function(eta_i, dose, vd, theta_tvcl, t) {
term <- (theta_tvcl * t * exp(eta_i)) / vd
derivative <- -term * f_pred(eta_i, dose, vd, theta_tvcl, t)
return(derivative)
}This is the definition of the second derivative function (reproduction of Equation 60):
function: f_double_prime()
# Define the second derivative of the structural model prediction function
f_double_prime <- function(eta_i, dose, vd, theta_tvcl, t) {
term <- (theta_tvcl * t * exp(eta_i)) / vd
second_derivative <- term * (term - 1) * f_pred(eta_i, dose, vd, theta_tvcl, t)
return(second_derivative)
}We now need to pay attention what R is actually returning in these functions. For all individuals we have multiple data points, so t is going to be a vector. This will propagate then throughout the calculations and the results/derivative/second_derivative object, which is being returned, will also be a vector.
Now we need to define two functions to reproduce Equation 68. Since finding the mode \(\eta_i^*\) is an optimization problem, we need to define it’s own objective function for which we are going to numerically solve for the maximum:
function: obj_fun_eta_i_star()
# Objective function for optimization to find eta_i_star
obj_fun_eta_i_star <- function(eta_i, y_i, t, theta_tvcl, vd, dose, sigma2, omega2, f_pred) {
f_pred_value <- f_pred(eta_i = eta_i, dose = dose, vd = vd, theta_tvcl = theta_tvcl, t = t)
term1 <- sum((y_i - f_pred_value)^2 / (2 * sigma2))
term2 <- eta_i^2 / (2 * omega2)
obj_value <- term1 + term2
return(obj_value)
}Since our optimizer function (optim) will actually minimize the objective function, we already previously turned the objective function into a minimization problem by negation (see Section 5.4.5). In the end it doesn’t matter if we maximize the positive version of the term or if we minimize the negative version given by Equation 68. The actual optimizer is then being encoded in a separate function and takes as an argument the MAP objective function we have defined earlier:
function: compute_eta_i_star()
# Define optimizer function to find eta_i_star
compute_eta_i_star <- function(y_i, t, theta_tvcl, vd, dose, sigma2, omega2, f_pred, eta_i_init = 0, obj_fun_eta_i_star) {
res <- optim(
par = eta_i_init,
fn = obj_fun_eta_i_star,
y_i = y_i,
t = t,
theta_tvcl = theta_tvcl,
vd = vd,
dose = dose,
sigma2 = sigma2,
omega2 = omega2,
f_pred = f_pred,
method = "BFGS"
)
eta_i_star <- res$par
return(eta_i_star)
}Please note that the compute_eta_i_star() function takes as arguments the functions which we have defined prior to that: f_pred() and obj_fun_eta_i_star(). Another hint: We need to find \(\eta_i^*\) for each individual. That’s why we’ll apply our function compute_eta_i_star() on an individual level and it will return a single value of \(\eta_i^*\). Please note that each individual has multiple observations and therefore obj_fun_eta_i_star() calculates the sum of the squared residual terms.
Now we need to define an R function for the second derivative \(g_i''(\eta_i)\), which is given by Equation 64. Again, we need to take the sum of the likelihood term to get a single value for each individual with multiple observations. Even with multiple observations, the prior term is only being accounted for once. This explains why with a larger number of observations the likelihood is going to dominate the prior.
function: gi_double_prime()
# Define second derivative of gi
gi_double_prime <- function(eta_i, y_i, t, theta_tvcl, vd, dose, sigma2, omega2) {
# Calculate f_pred, f_prime, and f_double_prime for all time points
f_pred_val <- f_pred(eta_i, dose, vd, theta_tvcl, t)
f_prime_val <- f_prime(eta_i, dose, vd, theta_tvcl, t)
f_double_prime_val <- f_double_prime(eta_i, dose, vd, theta_tvcl, t)
# Compute the numerator for each observation
numerator <- (-f_prime_val^2 + (y_i - f_pred_val) * f_double_prime_val)
# Divide by sigma^2 for each observation
term <- numerator / sigma2
# Sum the terms across all observations for the individual
sum_term <- sum(term)
# Subtract the term 1 / omega^2
second_derivative <- sum_term - (1 / omega2)
# return the second derivative
return(second_derivative)
}From here on, we only need to define one last function: the objective function, which brings all the pieces together.
When defining the objective function (see Equation 75), we are going to rely on all other functions defined above. Please note, that the ofv_function defined below will calculate the objective function value for a single individual. Later on we will have to loop over all individuals and sum up the OFV as defined in Equation 76.
function: ofv_function()
# Define the objective function OFV
ofv_function <- function(y_i, t, theta_tvcl, vd, dose, sigma2, omega2, f_pred, gi_double_prime, compute_eta_i_star, obj_fun_eta_i_star, eta_i_init = 0, return_val = "ofv") {
# Compute eta_i_star
eta_i_star <- compute_eta_i_star(
y_i = y_i,
t = t,
theta_tvcl = theta_tvcl,
vd = vd,
dose = dose,
sigma2 = sigma2,
omega2 = omega2,
f_pred = f_pred,
eta_i_init = eta_i_init,
obj_fun_eta_i_star = obj_fun_eta_i_star
)
# Compute f(eta_i_star)
f_pred_value <- f_pred(eta_i_star, dose, vd, theta_tvcl, t)
# Compute residual term
residual <- y_i - f_pred_value
residual_squared <- residual^2
# Compute the first term: ln(sigma^2)
term1 <- length(y_i) * log(sigma2)
# Compute the second term: (y_i - f(eta_i_star))^2 / sigma2
term2 <- sum(residual_squared) / sigma2
# Compute the third term: ln(omega^2)
term3 <- log(omega2)
# Compute the fourth term: (eta_i_star)^2 / omega2
term4 <- (eta_i_star^2) / omega2
# Compute gi''(eta_i_star)
gi_double_prime_value <- gi_double_prime(
eta_i = eta_i_star,
y_i = y_i,
t = t,
theta_tvcl = theta_tvcl,
vd = vd,
dose = dose,
sigma2 = sigma2,
omega2 = omega2
)
# Compute term5: ln of absolute value of gi_double_prime_value
term5 <- log(abs(gi_double_prime_value))
# Sum all terms to compute the objective function value
ofv <- term1 + term2 + term3 + term4 + term5
# return by default ofv, but we can also request to return the eta_i_star
if(return_val == "ofv"){
return(ofv)
} else if(return_val == "eta_i_star"){
return(eta_i_star)
}
}Great! Now we are all set to reproduce the objective function values for each iteration.
Let’s start with a little recap. Our simulated concentration-time data was given by this data frame:
# show simulated data
sim_data_reduced |>
select(ID, TIME, DV) |>
head() |>
mytbl()| ID | TIME | DV |
|---|---|---|
| 1 | 0.01 | 30.8160 |
| 1 | 3.00 | 24.5520 |
| 1 | 6.00 | 17.9250 |
| 1 | 12.00 | 10.1100 |
| 1 | 24.00 | 3.5975 |
| 2 | 0.01 | 31.4550 |
The following .ext file contained the information about the objective function values, which we are trying to reproduce in this chapter:
# show first row
ext_file |>
mytbl()| ITERATION | CL | V | RUV_VAR | IIV_VAR | OBJ |
|---|---|---|---|---|---|
| 0 | 0.100000 | 3.15 | 0.1 | 0.1500000 | 41.845437 |
| 1 | 0.168370 | 3.15 | 0.1 | 0.4839690 | -2.743076 |
| 2 | 0.163689 | 3.15 | 0.1 | 0.3881430 | -3.068198 |
| 3 | 0.216552 | 3.15 | 0.1 | 0.1465500 | -11.297115 |
| 4 | 0.216552 | 3.15 | 0.1 | 0.1465500 | -11.297115 |
| 5 | 0.253493 | 3.15 | 0.1 | 0.0862428 | -12.418728 |
| 6 | 0.243287 | 3.15 | 0.1 | 0.1171540 | -12.789118 |
| 7 | 0.246139 | 3.15 | 0.1 | 0.1111950 | -12.823615 |
| 8 | 0.246715 | 3.15 | 0.1 | 0.1099530 | -12.824589 |
| 9 | 0.246682 | 3.15 | 0.1 | 0.1100200 | -12.824593 |
| 10 | 0.246682 | 3.15 | 0.1 | 0.1100200 | -12.824593 |
Now we are going to loop over all iterations and calculate the objective function values for each individual. We will then sum up the individual objective function values to get the total objective function value for each iteration.
# define empty tibble
ofv_values <- tibble(ITERATION = numeric(), OBJ_R = numeric())
# define constants
DOSE <- 100
# loop over iterations
for(iter in 1:nrow(ext_file)){
# retrieve information from first row
TVCL <- ext_file |> slice(iter) |> pull(CL)
VD <- ext_file |> slice(iter) |> pull(V)
RUV_VAR <- ext_file |> slice(iter) |> pull(RUV_VAR)
IIV_VAR <- ext_file |> slice(iter) |> pull(IIV_VAR)
# create empty vector for individual ofv values
ofv_values_iter <- numeric()
# Loop over individuals
for(i in unique(sim_data_reduced$ID)){
# Filter data for individual i
data_i <- sim_data_reduced |>
filter(ID == i)
# Extract individual parameters
y_i <- data_i$DV
t <- data_i$TIME
# Compute the objective function value
ofv_i <- ofv_function(
y_i = y_i,
t = t,
theta_tvcl = TVCL,
vd = VD,
dose = DOSE,
sigma2 = RUV_VAR,
omega2 = IIV_VAR,
f_pred = f_pred,
gi_double_prime = gi_double_prime,
compute_eta_i_star = compute_eta_i_star,
obj_fun_eta_i_star = obj_fun_eta_i_star
)
# append to vector
ofv_values_iter <- c(ofv_values_iter, ofv_i)
}
# calculate sum of ofv_values
OFV_sum <- sum(ofv_values_iter)
# store in tibble with add row
ofv_values <- ofv_values |>
add_row(ITERATION = iter-1, OBJ_R = OFV_sum)
}
# add columns of ofv_values (join) to ext_file
ext_file <- ext_file |>
left_join(ofv_values, by = "ITERATION")With the last lines of code, we have joined our estimated objective function values to the .ext file and can now compare the reproduced objective function values with the original ones:
# show ext_file
ext_file |>
mutate(DIFF = OBJ_R - OBJ) |>
mytbl()| ITERATION | CL | V | RUV_VAR | IIV_VAR | OBJ | OBJ_R | DIFF |
|---|---|---|---|---|---|---|---|
| 0 | 0.100000 | 3.15 | 0.1 | 0.1500000 | 41.845437 | 41.845437 | 0.00e+00 |
| 1 | 0.168370 | 3.15 | 0.1 | 0.4839690 | -2.743076 | -2.743092 | -1.64e-05 |
| 2 | 0.163689 | 3.15 | 0.1 | 0.3881430 | -3.068198 | -3.068141 | 5.70e-05 |
| 3 | 0.216552 | 3.15 | 0.1 | 0.1465500 | -11.297115 | -11.297124 | -9.10e-06 |
| 4 | 0.216552 | 3.15 | 0.1 | 0.1465500 | -11.297115 | -11.297124 | -9.10e-06 |
| 5 | 0.253493 | 3.15 | 0.1 | 0.0862428 | -12.418728 | -12.418735 | -7.90e-06 |
| 6 | 0.243287 | 3.15 | 0.1 | 0.1171540 | -12.789118 | -12.789115 | 3.20e-06 |
| 7 | 0.246139 | 3.15 | 0.1 | 0.1111950 | -12.823615 | -12.823615 | 2.00e-07 |
| 8 | 0.246715 | 3.15 | 0.1 | 0.1099530 | -12.824589 | -12.824589 | -2.00e-07 |
| 9 | 0.246682 | 3.15 | 0.1 | 0.1100200 | -12.824593 | -12.824594 | -1.00e-07 |
| 10 | 0.246682 | 3.15 | 0.1 | 0.1100200 | -12.824593 | -12.824594 | -1.00e-07 |
In this table, the OBJ column represents the values from the NONMEM output, while OBJ_R represents our reproduced values. We can now compare the two columns to see if we have done a good job in reproducing the objective function values!
In general, I would say the reproduced values match the original values quite well. There are some small differences, mainly associated to the fifth digit after the decimal point. Of course there is always the possibility that I have made a mistake in the implementation, but I rather expect the differences to be related to e.g., the difference between analytical solution of the second derivative and the numerical approximation in NONMEM.
Now we can go ahead and try to plot the surface of the objective function. For this purpose, we are going to create a grid of possible combinations within a certain range of \(\theta_{TVCL}\) and \(\omega^2\). We will then calculate the objective function value for each grid element and plot the surface. We will start with the grid generation.
In order to get a nice surface plot, we will plot all possible combination for \(\theta_{TVCL}\) and \(\omega^2\) within a certain range. Here is the head of the respective grid table:
# Define the grid
theta_tvcl_values <- seq(0.01, 0.6, length.out = 100)
omega2_values <- seq(0.01, 0.8, length.out = 100)
grid <- expand.grid(theta_tvcl = theta_tvcl_values, omega2 = omega2_values)
# show grid
grid |>
head() |>
mytbl()| theta_tvcl | omega2 |
|---|---|
| 0.0100000 | 0.01 |
| 0.0159596 | 0.01 |
| 0.0219192 | 0.01 |
| 0.0278788 | 0.01 |
| 0.0338384 | 0.01 |
| 0.0397980 | 0.01 |
In a next step, we can calculate the objective function value for each grid element.
Now, we will loop over all grid elements and calculate the objective function value for each combination of \(\theta_{TVCL}\) and \(\omega^2\). We will then store the results in a tibble and convert it to a matrix for plotting.
# Define empty tibble for grid + OFV values
ofv_grid_values <- tibble(THETA_TVCL = numeric(), OMEGA2 = numeric(), OBJ = numeric())
# Loop over grid elements
for(i in 1:nrow(grid)){
# Extract theta_tvcl and omega2
theta_tvcl <- grid |> slice(i) |> pull(theta_tvcl)
omega2 <- grid |> slice(i) |> pull(omega2)
# create empty vector for individual ofv values
ofv_values_iter <- numeric()
# Loop over individuals
for(i in unique(sim_data_reduced$ID)){
# Filter data for individual i
data_i <- sim_data_reduced |>
filter(ID == i)
# Extract individual parameters
y_i <- data_i$DV
t <- data_i$TIME
# Compute the objective function value
ofv_i <- ofv_function(
y_i = y_i,
t = t,
theta_tvcl = theta_tvcl,
vd = VD,
dose = DOSE,
sigma2 = RUV_VAR,
omega2 = omega2,
f_pred = f_pred,
gi_double_prime = gi_double_prime,
compute_eta_i_star = compute_eta_i_star,
obj_fun_eta_i_star = obj_fun_eta_i_star
)
# append to vector
ofv_values_iter <- c(ofv_values_iter, ofv_i)
}
# calculate sum of ofv_values
OFV_sum <- sum(ofv_values_iter)
# store in tibble with add row
ofv_grid_values <- ofv_grid_values |>
add_row(THETA_TVCL = theta_tvcl, OMEGA2 = omega2, OBJ = OFV_sum)
}
# Convert to matrix for z-values
x_unique <- unique(ofv_grid_values$THETA_TVCL)
y_unique <- unique(ofv_grid_values$OMEGA2)
z_matrix <- matrix(ofv_grid_values$OBJ, nrow = length(x_unique), byrow = TRUE)Great. Now we have everything available to plot the 3D surface and to illustrate the steps which the estimation algorithm has taken to find the maximum likelihood estimate:
# with tracer
# Create 3D surface plot using plotly
plot_ly(
x = ~x_unique,
y = ~y_unique,
z = ~z_matrix,
type = "surface",
cmin = -20, cmax = 60, name = "Surface",
showscale = TRUE,
colorbar = list(title = "OFV")
) |>
add_trace(
data = ext_file,
x = ~CL,
y = ~IIV_VAR,
z = ~OBJ,
type = 'scatter3d',
mode = 'markers',
marker = list(symbol = 'cross', color = 'red', size = 8),
name = "NONMEM"
) |>
add_trace(
data = ext_file,
x = ~CL,
y = ~IIV_VAR,
z = ~OBJ,
type = 'scatter3d',
mode = 'lines',
line = list(color = 'black', width = 3),
connectgaps = TRUE,
name = "NONMEM"
) |>
layout(
scene = list(
xaxis = list(title = "Typical Clearance"),
yaxis = list(title = "IIV Variance"),
zaxis = list(title = "Objective Function Value", range = c(-20, 60))
)
)We can nicely see the surface and also the location of the maximum likelihood estimate. The red crosses represent the individual iterations of the estimation algorithm. The black line connects the individual iterations in the order they were performed. Apparently the optimization algorithm in NONMEM was quite efficient in finding a suitable path to the maximum likelihood estimate.
So far, we have reproduced the NONMEM objective function at each iteration of the estimation, plotted the objective function surface, and observed how NONMEM navigated the parameter space to locate the maximum likelihood estimate. However, we have relied on the information of the .ext file, so all the steps of the optimization problem were pre-defined. Now, we want to attempt a similar estimation process directly in R, using the native optim() function. Our aim is to see whether we arrive at similar final estimates as those obtained by NONMEM.
To perform the estimation entirely in R, we will encapsulate much of our previous logic into a single objective function which takes the current set of parameters as a vector (starting with the initials) and is returning the sum of the objective function across all individuals. This sum is what we will ask optim() in R to minimize by searching the parameter space. Essentially, nothing changes but we have to wrap everything in one single function which can be passed to optim().
function: ofv_function()
# define objective function for r-based parameter optimization
param_est_obj <- function(par,
sim_data_reduced,
VD,
DOSE,
RUV_VAR,
f_pred,
gi_double_prime,
compute_eta_i_star,
obj_fun_eta_i_star) {
# Extract theta_tvcl and omega2
theta_tvcl <- par[[1]]
omega2 <- par[[2]]
# create empty vector for individual ofv values
ofv_values_iter <- numeric()
# Loop over individuals
for(i in unique(sim_data_reduced$ID)){
# Filter data for individual i
data_i <- sim_data_reduced |>
filter(ID == i)
# Extract individual parameters
y_i <- data_i$DV
t <- data_i$TIME
# Compute the objective function value
ofv_i <- ofv_function(
y_i = y_i,
t = t,
theta_tvcl = theta_tvcl,
vd = VD,
dose = DOSE,
sigma2 = RUV_VAR,
omega2 = omega2,
f_pred = f_pred,
gi_double_prime = gi_double_prime,
compute_eta_i_star = compute_eta_i_star,
obj_fun_eta_i_star = obj_fun_eta_i_star
)
# append to vector
ofv_values_iter <- c(ofv_values_iter, ofv_i)
}
# calculate sum of ofv_values
OFV_sum <- sum(ofv_values_iter)
# return OFV sum
return(OFV_sum)
}Great! Now we have the param_est_obj() function ready and it can be passed to the optimizer to start our own estimation.
To perform the estimation, we will pass the param_est_obj() function to optim function in R. For this part, we will select initial values that are close to the actual parameter estimates and additionally apply lower and upper bounds using the L-BFGS-B method. While playing around with the initial values, it became evident that the optim function and our current setup are considerably more sensitive to initial values than NONMEM. When the initial values were too far from the true estimates or when the optimizer was run without boundaries, I often encountered numerical issues, leading to termination of the estimation process. In contrast, NONMEM proved to be significantly more robust, suggesting that its optimizer is finely tuned for the pharmacometric problems we typcially face. In contrast, optim is rather a general purpose optimizer.
# Starting guesses for theta_tvcl and omega2
initials <- c(0.2, 0.1)
# perform estimation
optim_res <- optim(
par = initials,
fn = param_est_obj,
sim_data_reduced = sim_data_reduced,
VD = ext_file$V |> unique(),
DOSE = DOSE,
RUV_VAR = ext_file$RUV_VAR |> unique(),
f_pred = f_pred,
gi_double_prime = gi_double_prime,
compute_eta_i_star= compute_eta_i_star,
obj_fun_eta_i_star= obj_fun_eta_i_star,
method = "L-BFGS-B",
lower = rep(0.001, length(initials)),
upper = rep(1000, length(initials)),
hessian = TRUE,
control = list(
maxit = 10000,
factr = 1e-7,
pgtol = 1e-7,
trace = 1,
REPORT = 1
)
)iter 1 value -12.819995
iter 2 value -12.822838
iter 3 value -12.824104
iter 4 value -12.824484
iter 5 value -12.824594
iter 6 value -12.824594
iter 7 value -12.824594
iter 8 value -12.824594
final value -12.824594
convergedThe optimization successfully converged and we can also see the trace of the optimization problem. The optim_res object now contains all the information we need about the optimization:
# show optim_res object
optim_res$par
[1] 0.2466737 0.1100256
$value
[1] -12.82459
$counts
function gradient
16 16
$convergence
[1] 0
$message
[1] "CONVERGENCE: NORM OF PROJECTED GRADIENT <= PGTOL"
$hessian
[,1] [,2]
[1,] 2.979341e+03 -0.003861313
[2,] -3.861313e-03 821.681234002Great! We can now compare the parameter estimates against the NONMEM estimates to see how well we were doing.
To compare our results against NONMEM, we will use the final iteration from the .ext file to extract the final parameter estimates. We will then incorporate the information obtained from the optim object in R, allowing us to directly compare the two sets of parameter estimates.
# retrieve final parameter estimates from NM
nm_par_est <- ext_file |>
filter(ITERATION == max(ext_file$ITERATION)) |>
select(CL, IIV_VAR, OBJ) |>
rename(
"CL_NM" = CL,
"IIV_VAR_NM" = IIV_VAR,
"OBJ_NM" = OBJ
) |>
mutate(
CL_R = optim_res$par[[1]],
IIV_VAR_R = optim_res$par[[2]],
OBJ_R = optim_res$value,
CL_DIFF = CL_R - CL_NM,
IIV_VAR_DIFF = IIV_VAR_R - IIV_VAR_NM,
OBJ_DIFF = OBJ_NM - OBJ_R
) |>
select(
CL_NM, CL_R, CL_DIFF, IIV_VAR_NM, IIV_VAR_R, IIV_VAR_DIFF, OBJ_NM, OBJ_R, OBJ_DIFF
)
# show
nm_par_est |>
mytbl()| CL_NM | CL_R | CL_DIFF | IIV_VAR_NM | IIV_VAR_R | IIV_VAR_DIFF | OBJ_NM | OBJ_R | OBJ_DIFF |
|---|---|---|---|---|---|---|---|---|
| 0.246682 | 0.2466737 | -8.3e-06 | 0.11002 | 0.1100256 | 5.6e-06 | -12.82459 | -12.82459 | 3e-07 |
Our R-based implementation achieves convergence to parameter estimates that are very similar to those obtained with NONMEM.
To assess parameter precision, NONMEM performs a covariance step ($COVARIANCE) where it numerically approximates and inverts the Hessian, the second derivative matrix of the objective function evaluated at the final parameter estimates. Please note: This second derivative form the $COVARIANCE step is not the same second derivative as the one for \(g_i(\eta_i)\) which we have calculated in Section 5.4.4 during the construction of the objective function. This time, we focus on the second derivative matrix of the objective function itself and the second derivative of \(g_i(\eta_i)\) is only part of the objective function.
The $COVARIANCE process (if successful) produces the variance-covariance matrix of the parameter estimates, which is used to derive standard errors and parameter correlations. Similarly, in our R-based implementation, we can utilize the Hessian returned by the optim function.
We can directly retrieve the hessian matrix from the optim_res object by assessing it via $hessian. Please note, that we did request the hessian during optimization with hessian = TRUE. This is the output:
# store hessian
hessian <- optim_res$hessian
# show
hessian [,1] [,2]
[1,] 2.979341e+03 -0.003861313
[2,] -3.861313e-03 821.681234002We can now go ahead and solve the matrix to get its inverse. The inverse of the Hessian serves as an approximation to the covariance matrix.
# Standard errors (square root of variances)
inverse_hessian <- optim_res$hessian |> solve()
# show inverse hessian
inverse_hessian [,1] [,2]
[1,] 3.356447e-04 1.577289e-09
[2,] 1.577289e-09 1.217017e-03We are mainly interested in the variances for now, so we only care about the diagonals. We are going to retrieve the diagonals and store them alongside the parameter estimates inside a tibble:
# get diagonal elements
variances_vec <- diag(inverse_hessian)
# define row
row1 <- tibble(
PAR = "TVCL",
EST_R = optim_res$par[[1]],
VAR_R = variances_vec[[1]]
)
# define row
row2 <- tibble(
PAR = "IIV_VAR",
EST_R = optim_res$par[[2]],
VAR_R = variances_vec[[2]]
)
# bind rows for parameter precicsion table
par_prec <- bind_rows(row1, row2)
# show
par_prec |>
mytbl()| PAR | EST_R | VAR_R |
|---|---|---|
| TVCL | 0.2466737 | 0.0003356 |
| IIV_VAR | 0.1100256 | 0.0012170 |
We now have the parameter estimates and the associated variances stored in a single tibble.
Now we can go ahead to calculate the standard error. The standard errors are the square root of the variances, so we can add a column with SE_R:
# calculate standard errors
par_prec <- par_prec |>
mutate(
SE_R = sqrt(VAR_R)
)
# show
par_prec |>
mytbl()| PAR | EST_R | VAR_R | SE_R |
|---|---|---|---|
| TVCL | 0.2466737 | 0.0003356 | 0.0183206 |
| IIV_VAR | 0.1100256 | 0.0012170 | 0.0348858 |
Finally, the relative standard errors (RSE) can be calculated based on the standard error and the estimate itself. We are going to add RSE%_R to the tibble:
# Calculate relative standard error
par_prec <- par_prec |>
mutate("RSE%_R" = (SE_R / EST_R)*100)
# show table
par_prec |>
mytbl()| PAR | EST_R | VAR_R | SE_R | RSE%_R |
|---|---|---|---|---|
| TVCL | 0.2466737 | 0.0003356 | 0.0183206 | 7.427062 |
| IIV_VAR | 0.1100256 | 0.0012170 | 0.0348858 | 31.706964 |
Apparently, the parameter precision for the typical value of clearance is much higher than the variance estimate for the inter-individual variability. However, both estimates would be within an acceptable range and parameter precision would not be a particular concern.
In the previous steps, we have assessed the parameter precision of our R-based optimization run. Now, we want to compare the results against our reference solution. In a first step, we are going to load in the data from the .cov file from NONMEM, which contains the variance-covariance matrix of the parameter estimates from the estimation step
# load nonmem .cov output
nm_cov <- nonmem2R::covload(
model = paste0(base_path, "models/estimation/1cmt_iv_est.cov"),
theta.only = FALSE
) |>
as_tibble()
# show
nm_cov |>
mytbl()| THETA1 | THETA2 | OMEGA.1.1. | SIGMA.1.1. |
|---|---|---|---|
| 0.0006715 | 0 | 0.0007977 | 0 |
| 0.0000000 | 0 | 0.0000000 | 0 |
| 0.0007977 | 0 | 0.0023749 | 0 |
| 0.0000000 | 0 | 0.0000000 | 0 |
This is a representation of the covariance matrix from NONMEM. We are now going to perform the same steps as done above and then augment the results with the R-based results to compare both results.
# augment table
par_prec <- par_prec |>
mutate(
EST_NM = c(nm_par_est$CL_NM, nm_par_est$IIV_VAR_NM),
VAR_NM = c(nm_cov$THETA1[[1]], nm_cov$OMEGA.1.1.[[3]]),
SE_NM = sqrt(VAR_NM),
"RSE%_NM" = (SE_NM/EST_NM)*100,
"RSE%_DIFF" = `RSE%_R` - `RSE%_NM`
) |>
select(PAR, EST_R, EST_NM, VAR_R, VAR_NM, SE_R, SE_NM, `RSE%_R`, `RSE%_NM`, `RSE%_DIFF`)
# show table
par_prec |>
mytbl()| PAR | EST_R | EST_NM | VAR_R | VAR_NM | SE_R | SE_NM | RSE%_R | RSE%_NM | RSE%_DIFF |
|---|---|---|---|---|---|---|---|---|---|
| TVCL | 0.2466737 | 0.246682 | 0.0003356 | 0.0006715 | 0.0183206 | 0.0259135 | 7.427062 | 10.50480 | -3.077739 |
| IIV_VAR | 0.1100256 | 0.110020 | 0.0012170 | 0.0023749 | 0.0348858 | 0.0487325 | 31.706964 | 44.29425 | -12.587288 |
With our R-based reproduction, we can capture the general trend of higher parameter imprecision for $OMEGA estimates. However, we are unable to replicate the exact numerical values from the NONMEM output. The differences in relative standard errors (RSEs) are substantial, with R showing a consistent bias toward lower RSEs compared to NONMEM. It remains unclear whether these discrepancies indicate an error in my implementation or if they can be attributed solely to differences in how the Hessian matrix is approximated in the maximum likelihood estimate. I personally lack enough knowledge about the specific numerical approximation methods used by NONMEM versus the optim function in R, and I am unsure whether such differences are expected or not.
Individual ETAs can be calculated using Bayesian maximum a-posteriori estimation, a process commonly executed during the POSTHOC step in NONMEM. Essentially, this involves calculating the individual \(\eta_i^*\) value, which we previously computed while constructing the objective function. To validate our approach, we can perform an additional sanity check by comparing the individual ETAs derived from our custom function—using the maximum likelihood estimates—with those generated by NONMEM’s $POSTHOC step.
In a first step, we are going to read in the sdtab which contains the individual realization of the random variable, ETA1. We are then only keeping one distinct row per ID.
# load nonmem output with posthoc ETA
sdtab <- read_nm_table(paste0(base_path, "models/estimation/estim_out"))
# summarise nonmem eta_i values
nm_eta_i_star_values <- sdtab |>
select(ID, ETA1) |>
distinct() |>
rename(ETA1_NM = ETA1)
# show table
nm_eta_i_star_values |>
mytbl()| ID | ETA1_NM |
|---|---|
| 1 | 0.173900 |
| 2 | -0.110320 |
| 3 | -0.043933 |
| 4 | -0.153930 |
| 5 | 0.725750 |
| 6 | -0.033077 |
| 7 | -0.349690 |
| 8 | -0.427840 |
| 9 | -0.183560 |
| 10 | 0.402510 |
Now it is time to reproduce the Empirical Bayes Estimates (EBE) or Maximum A Posteriori (MAP) step using the custom function we defined earlier when constructing the objective function. For this, we will use the final parameter estimates obtained at convergence during our estimation process.
# define iter as maximum
iter <- nrow(ext_file)
# retrieve information from first row
TVCL <- ext_file |> slice(iter) |> pull(CL)
VD <- ext_file |> slice(iter) |> pull(V)
RUV_VAR <- ext_file |> slice(iter) |> pull(RUV_VAR)
IIV_VAR <- ext_file |> slice(iter) |> pull(IIV_VAR)
# define constants
DOSE <- 100
# define initials
eta_i_init <- 0
# create empty list for individual eta_i_star values
eta_i_star_list <- list()
# Loop over individuals
for(i in unique(sim_data_reduced$ID)){
# Filter data for individual i
data_i <- sim_data_reduced |>
filter(ID == i)
# Extract individual parameters
y_i <- data_i$DV
t <- data_i$TIME
# compute eta_i_star
eta_i_star <- compute_eta_i_star(
y_i = y_i,
t = t,
theta_tvcl = TVCL,
vd = VD,
dose = DOSE,
sigma2 = RUV_VAR,
omega2 = IIV_VAR,
f_pred = f_pred,
eta_i_init = eta_i_init,
obj_fun_eta_i_star = obj_fun_eta_i_star
)
# append to vector
eta_i_star_list[[i]] <- tibble(
ID = i,
ETA1_R = eta_i_star
)
}
# store in tibble with add row
eta_i_star_values <- bind_rows(eta_i_star_list)
# show the results
eta_i_star_values |>
mytbl()| ID | ETA1_R |
|---|---|
| 1 | 0.1738965 |
| 2 | -0.1103184 |
| 3 | -0.0439348 |
| 4 | -0.1539363 |
| 5 | 0.7257483 |
| 6 | -0.0330794 |
| 7 | -0.3496945 |
| 8 | -0.4278383 |
| 9 | -0.1835616 |
| 10 | 0.4025086 |
Now that we have the estimates ready for both NONMEM and R, we can compare both and calculate the difference.
# left_join
eta_i_star_values <- eta_i_star_values |>
left_join(nm_eta_i_star_values, by = "ID") |>
mutate(DIFF = ETA1_R - ETA1_NM)
# show tibble
eta_i_star_values |>
mytbl()| ID | ETA1_R | ETA1_NM | DIFF |
|---|---|---|---|
| 1 | 0.1738965 | 0.173900 | -3.5e-06 |
| 2 | -0.1103184 | -0.110320 | 1.6e-06 |
| 3 | -0.0439348 | -0.043933 | -1.8e-06 |
| 4 | -0.1539363 | -0.153930 | -6.3e-06 |
| 5 | 0.7257483 | 0.725750 | -1.7e-06 |
| 6 | -0.0330794 | -0.033077 | -2.4e-06 |
| 7 | -0.3496945 | -0.349690 | -4.5e-06 |
| 8 | -0.4278383 | -0.427840 | 1.7e-06 |
| 9 | -0.1835616 | -0.183560 | -1.6e-06 |
| 10 | 0.4025086 | 0.402510 | -1.4e-06 |
The differences between the two implementations are tiny, only showing up in distant decimal places. This gives me confidence that our MAP objective function is working as it should.
What a journey! We have successfully implemented the objective function of a simple 1-compartment iv bolus model in R - hopefully without too many mistakes or violations of mathematical/statistical notation. Since we have chosen to perform this exercise on quite a simple model, we were able to plot the 3D surface of the objective function to visually see the path the optimizer in NONMEM was taking. Subsequently, we have performed our own estimation using the optim function in R and also replicated the COVARIANCE and POSTHOC step. While we can’t say with certainty that our attempt was fully successful, it appears at least plausible. And with that, I am happy to wrap up this already far-too-long blog post.
# display session info
sessionInfo()R version 4.3.0 (2023-04-21 ucrt)
Platform: x86_64-w64-mingw32/x64 (64-bit)
Running under: Windows 10 x64 (build 19045)
Matrix products: default
locale:
[1] LC_COLLATE=German_Germany.utf8 LC_CTYPE=German_Germany.utf8
[3] LC_MONETARY=German_Germany.utf8 LC_NUMERIC=C
[5] LC_TIME=German_Germany.utf8
time zone: Europe/Berlin
tzcode source: internal
attached base packages:
[1] stats graphics grDevices utils datasets methods base
other attached packages:
[1] plotly_4.10.3 tidyr_1.3.1 xpose4_4.7.2 lattice_0.21-8
[5] kableExtra_1.3.4 readr_2.1.5 ggplot2_3.5.1 dplyr_1.1.4
loaded via a namespace (and not attached):
[1] gtable_0.3.4 xfun_0.45 nonmem2R_0.2.5
[4] htmlwidgets_1.6.4 latticeExtra_0.6-30 tzdb_0.4.0
[7] vctrs_0.6.5 tools_4.3.0 crosstalk_1.2.0
[10] generics_0.1.3 parallel_4.3.0 tibble_3.2.1
[13] fansi_1.0.6 highr_0.10 pkgconfig_2.0.3
[16] data.table_1.15.4 RColorBrewer_1.1-3 webshot_0.5.5
[19] lifecycle_1.0.4 splines2_0.5.3 deldir_2.0-4
[22] compiler_4.3.0 farver_2.1.1 stringr_1.5.1
[25] munsell_0.5.0 codetools_0.2-19 htmltools_0.5.8.1
[28] yaml_2.3.9 lazyeval_0.2.2 pillar_1.9.0
[31] crayon_1.5.3 MASS_7.3-58.4 iterators_1.0.14
[34] foreach_1.5.2 tidyselect_1.2.1 rvest_1.0.3
[37] digest_0.6.36 mvtnorm_1.2-2 stringi_1.8.4
[40] reshape2_1.4.4 purrr_1.0.2 labeling_0.4.3
[43] splines_4.3.0 rprojroot_2.0.4 fastmap_1.1.1
[46] grid_4.3.0 here_1.0.1 colorspace_2.1-0
[49] cli_3.6.3 magrittr_2.0.3 utf8_1.2.4
[52] withr_3.0.0 scales_1.3.0 bit64_4.0.5
[55] rmarkdown_2.26 httr_1.4.7 jpeg_0.1-10
[58] interp_1.1-6 bit_4.0.5 gridExtra_2.3
[61] png_0.1-8 hms_1.1.3 gam_1.22-2
[64] evaluate_0.23 knitr_1.46 viridisLite_0.4.2
[67] rlang_1.1.4 Rcpp_1.0.12 glue_1.7.0
[70] xml2_1.3.6 svglite_2.1.3 rstudioapi_0.16.0
[73] vroom_1.6.5 jsonlite_1.8.8 plyr_1.8.8
[76] R6_2.5.1 systemfonts_1.0.5 We only need to approximate \(g_i()\) if we cannot explicitly calculate that integral. If we would be in a linear setting (which we are not), we wouldn’t need any approximation and could directly work with it.↩︎
Remember: We actually deal with a latent, unobserved variable.↩︎
They are defined for the case of \(\eta_i^*\), but here we need the more general form of \(\eta_i\). But the expression itself is the same.↩︎
@online{klose2025,
author = {Klose, Marian},
title = {My Attempt to Understand the {NLME} Estimation Algorithm
Behind {NONMEM}},
date = {2025-01-11},
url = {https://marian-klose.com/posts/understanding_nlme_estimation/index.html},
langid = {en}
}