Code
# load packages
library(dplyr)
library(ggplot2)
library(readr)
library(kableExtra)
library(xpose4)
library(tidyr)March 31, 2025
Bayesian estimation is a widely-used method in pharmacometrics. Many pharmacometricians utilize individual predictions (IPRED) in their diagnostics, which represent simulations based on the maximum a-posteriori (MAP) estimates 1. These estimates essentially represent the mode of the so-called posterior distribution, which combines prior knowledge about the population and new evidence about the particular individual at hand (more to that later). MAP estimates also play a crucial role in Model-Informed Precision Dosing (MIPD), where one aims to predict the concentration-time profile of an individual, given a pharmacokinetic NLME model and a set of drug concentrations measured through a Therapeutic Drug Monitoring (TDM) program. During model building, the underlying individualized ETAs are often used for covariate screening, provided that shrinkage permits it. As you can see, Bayesian estimation is quite prominent in pharmacometric workflows. Thomas Bayes would be proud of us!

In many scenarios, these Bayesian calculations happen automatically under the hood when fitting pharmacometric models (e.g., in NONMEM), making it quite easy to use Bayesian estimates without exploring the underlying concepts and calculations. I myself did this for quite some time. Reproducing calculations through equations is often the best way to grasp the underlying principles. Therefore, I have decided to write this blogpost, in which I want to explain the Bayesian idea and reproduce a simple Bayesian MAP estimation in R. I will mainly focus on the point estimates of the posterior distribution (MAP or EBE). Addressing the full posterior distribution is also important and might be covered in a future post. There are other nice blogposts which cover full Bayesian approaches in more detail, such as Navarro (2023).
Please note: These are just my personal reflections and interpretations of Bayesian concepts. I cannot guarantee that my explanations, equations, or terminology are flawless. If you notice any inaccuracies, please let me know so I can correct them!
Let me briefly outline how I structured this blogpost. The overall goal is to better understand the Bayesian concept behind MAP estimation and to derive an individualized clearance estimate for a virtual patient using R, step by step.
I start with my own little introduction of the Bayesian idea (Section 3) using a real-world example and define the key components—prior, likelihood, and posterior.
This is then followed by a pharmacometric example using a simulated dataset (from my previous blogpost) and a simple one-compartment i.v. bolus PK model as reference (Section 4). This section also includes our NONMEM reference solution which is later used to validate our calculations in R.
Next, we try to explore the Bayesian theory a bit more, dealing with the mathematical formulation of MAP estimation and explaining how the prior and likelihood combine to form the posterior (Section 5).
Afterwards, we move on to the R-based MAP reproduction (Section 6). We implement the prior and likelihood functions, combine them into an optimization routine, and estimate the individual parameter from scratch. Finally, we are able to compare the R-based result to the NONMEM output and visualize how prior, likelihood, and posterior interact.
With that being said, let’s get started!
I would say that many of us naturally think Bayesian, even if we are not aware of it or if we don’t label it that way. At its core, Bayesian statistics is about updating your beliefs once new data or information becomes available. Let’s consider an example from the real-world to illustrate this idea.
Imagine you drive to work every day. If someone would ask you “How long will it take you to get to work tomorrow?”, you would probably have a good idea, simply based on your past experiences. 30 minutes might be your best guess, but would you bet money that it will be exactly 30 minutes? Probably not, as you will always have some uncertainty associated with it. Perhaps something between 20 and 40 minutes would be reasonable based on your previous trips. Now, let’s assume you get into your car the next morning and after 25 minutes, you have made it halfway.

Would you stick to your initial belief that it will take you 30 minutes? Probably not, you would likely revise it (or try to break all speed limits). But would you simply double the 25 minutes to predict a 50-minute commute? This is also unlikely, given your experience suggesting that 40 minutes is usually the upper limit. So, maybe you would adjust your estimate to 38 minutes, assuming that the traffic will get better soon. This is Bayesian thinking in action: Updating your beliefs with new data. But so far without any equation and rather based on gut-feeling.
Now, let’s map this real-world scenario to some Bayesian terminology. There are three key components in every Bayesian analysis:
Bayesian analysis starts with a prior, which you revise using new data (likelihood) to obtain the posterior. In pharmacometrics, we often encounter two levels of complexity when it comes to Bayes:
Many pharmacometricians use MAP estimates due to their computational simplicity and their direct integration into standard NLME routines, while full Bayesian methods offer a more comprehensive view by integrating uncertainty even after new data became available. Full Bayesian methods are more and more used in the field, also thanks to some nice tutorials by Margossian, Zhang, and Gillespie (2022) for Stan/Torsten and by Johnston et al. (2024) for NONMEM itself, both from the Metrum Research Group.
So, what role does Bayesian methodology play in pharmacometrics? Obviously it is not about optimizing your commute. Instead, we typically use Bayesian estimation to individualize the model parameters for a given individual \(i\), which has a set of unique observations \(Y_{i}\). This concept was first introduced to the pharmacometric community by Sheiner, Rosenberg, and Melmon (1972), if I am not mistaken. On the one hand, MAP estimation happens during model building, at each iteration step 2 and then after the actual estimation has finished, at the POSTHOC step. On the other hand, it is also used in MIPD settings as described above. The approach remains the same, and we will later have a look at a simple pharmacokinetic example to illustrate this.
So far we used a relatable example rather focusing on the intuition behind Bayesian thinking. Now we want to dive a bit into the mathematics behind it to be able to formally reproduce a simple Bayesian MAP estimation in R.
Without data, no Bayesian parameter individualization. For our MAP estimation, we are using the same simulated data set I have defined in the previous blogpost about NLME modelling. See Klose (2025) for more details about this data set. Let’s start by loading the simulated concentration-time data and showing the head of the data set:
| ID | TIME | EVID | AMT | RATE | DV | MDV |
|---|---|---|---|---|---|---|
| 1 | 0.00 | 1 | 100 | 0 | 0.0000 | 1 |
| 1 | 0.01 | 0 | 0 | 0 | 30.8160 | 0 |
| 1 | 3.00 | 0 | 0 | 0 | 24.5520 | 0 |
| 1 | 6.00 | 0 | 0 | 0 | 17.9250 | 0 |
| 1 | 12.00 | 0 | 0 | 0 | 10.1100 | 0 |
| 1 | 24.00 | 0 | 0 | 0 | 3.5975 | 0 |
We will focus on ID 5, which has lower simulated concentrations than the average individual, making it easier to observe differences between typical and individualized profiles. Here’s a plot to visualize these concentration-time profiles of ID 5 and the other IDs of the virtual population:
# show individual profiles
sim_data |>
filter(EVID == 0) |>
mutate(flag = if_else(ID == 5, "Reference", "Others")) |>
ggplot(aes(x=TIME, y=DV, group=ID, color=as.factor(flag))) +
geom_point()+
geom_line()+
theme_bw()+
scale_y_continuous(limits=c(0,NA))+
labs(x="Time after last dose [h]", y="Concentration [mg/L]")+
scale_color_manual("Individual", values=c("grey", "darkblue"))+
ggtitle("Simulated concentration time data after i.v. bolus injection")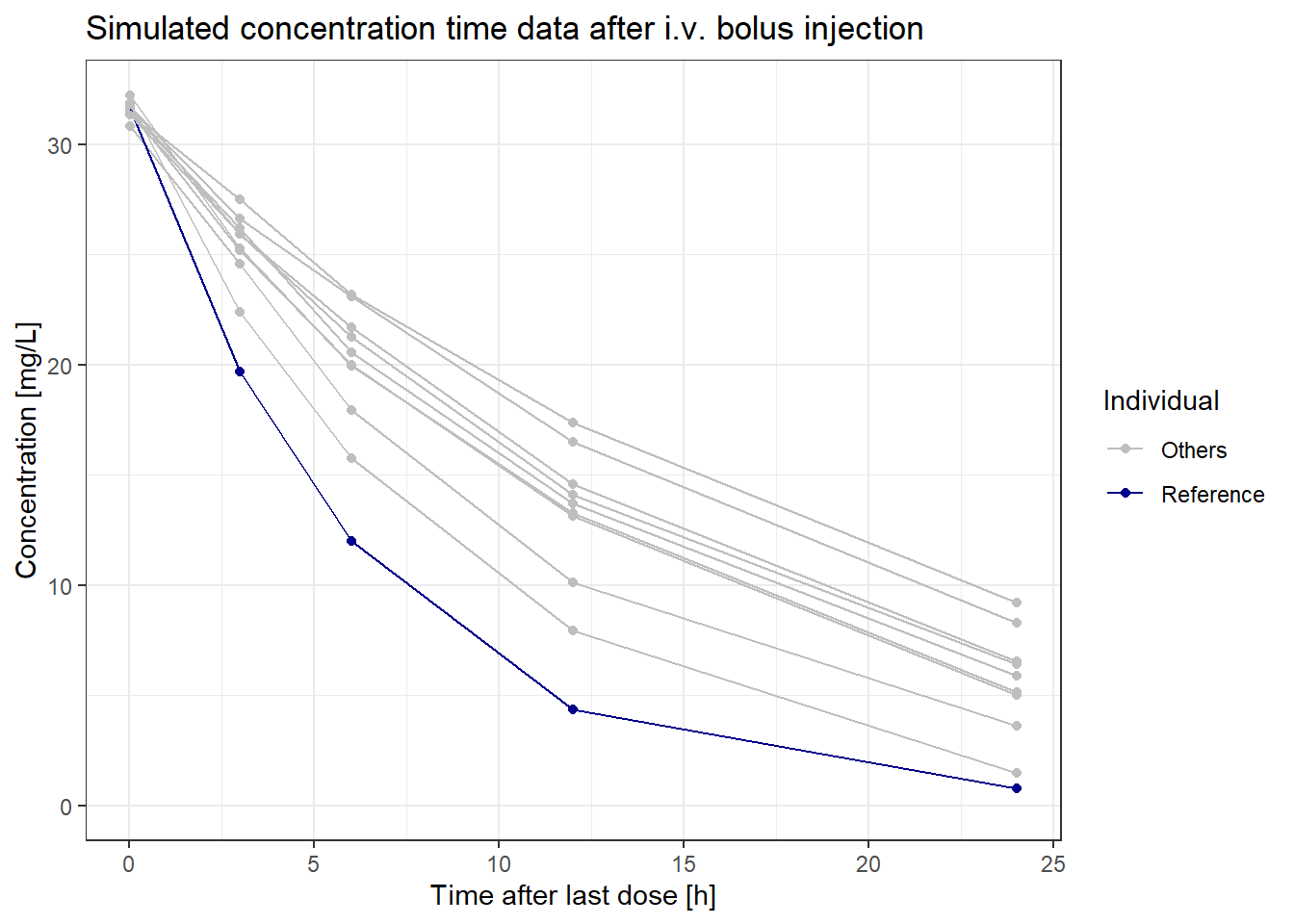
We will later need this data set when running the NONMEM-based MAP estimation, so we have to save it to file. Prior to that, we will filter the data set to only include the data for ID 5:
With that being done, we are all set to define the NLME model in NONMEM in a next step!
For our example and reference, we’ll use a simple one-compartment IV model with first-order kinetics, previously fitted to similar data (Klose (2025)). Here’s a sketch of the simple model structure:

Assuming our model is already fitted, our goal is to individualize parameters for ID 5. The model parameter estimates are based on the fitted model from the previous blogpost and are as follows:
In a next step, we will translate this into a NONMEM model. Note that we added a proportional error term to the previously used model to better illustrate the differences among prior, likelihood, and posterior distributions 3. For the same reason, we increased the additive error to 2 mg/L. Let’s store this information, along with the 100 mg intravenous bolus dose administered to the individual, in a list object for easy retrieval during subsequent calculations:
$tvcl
[1] 0.247
$tvvd
[1] 3.15
$omega2_CL
[1] 0.11
$sigma2_add
[1] 2
$sigma2_prop
[1] 0.5
$dose
[1] 100Great! Now we can go ahead and define the NONMEM model.
We have updated our NONMEM model slightly from the last blogpost:
1cmt_iv_map_est.mod
$PROBLEM 1cmt_iv_map_est
$INPUT ID TIME EVID AMT RATE DV MDV
$DATA C:\Users\mklose\Desktop\GitHub\personal-website\posts\bayes_map_estimation_r\data\sim_data_ID5.csv IGNORE=@
$SUBROUTINES ADVAN1 TRANS2
$PK
; define fixed effects parameters
CL = THETA(1) * EXP(ETA(1))
V = THETA(2)
; scaling
S1=V
$THETA
0.247 FIX ; 1 TVCL
3.15 FIX ; 2 TVV
$OMEGA
0.11 FIX ; 1 OM_CL
$SIGMA
0.50 FIX ; 1 SIG_PROP
2.00 FIX ; 2 SIG_ADD
$ERROR
; add residual unexplained variability
IPRED = F
Y = IPRED + IPRED * EPS(1) + EPS(2)
$ESTIMATION METHOD=1 INTERACTION MAXEVAL=0 SIGDIG=3 PRINT=1 NOABORT POSTHOC
$TABLE ID TIME EVID AMT RATE DV PRED IPRED MDV ETA1 CL NOAPPEND ONEHEADER NOPRINT FILE=map_estim_outWe have fixed the initial parameter estimates to the final estimates from before and incorporated a combined error model (as described above). By using MAXEVAL=0, we avoid any population parameter estimation and the model is simply being evaluated. The POSTHOC option computes individual MAP estimates as this is the core of our task. We need to make sure that we include the INTERACTION option in the $ESTIMATION block, as this tells NONMEM to include the effect of ETA on the residual error when performing MAP estimation 4. This is important as our error model now depends on IPRED, which in turn depends on ETA.
After running the model, we’ll read the output through map_estim_out:
| ID | TIME | EVID | AMT | RATE | DV | PRED | IPRED | MDV | ETA1 | CL |
|---|---|---|---|---|---|---|---|---|---|---|
| 5 | 0.00 | 1 | 100 | 0 | 0.00000 | 31.7460 | 31.7460 | 1 | 0.55194 | 0.42894 |
| 5 | 0.01 | 0 | 0 | 0 | 31.61900 | 31.7210 | 31.7030 | 0 | 0.55194 | 0.42894 |
| 5 | 3.00 | 0 | 0 | 0 | 19.66000 | 25.0920 | 21.1000 | 0 | 0.55194 | 0.42894 |
| 5 | 6.00 | 0 | 0 | 0 | 12.00700 | 19.8320 | 14.0230 | 0 | 0.55194 | 0.42894 |
| 5 | 12.00 | 0 | 0 | 0 | 4.33360 | 12.3890 | 6.1947 | 0 | 0.55194 | 0.42894 |
| 5 | 24.00 | 0 | 0 | 0 | 0.78148 | 4.8349 | 1.2088 | 0 | 0.55194 | 0.42894 |
The ETA1 (= \(\eta_i\)) value represents the individual random effect, while CL (= \(CL_i\)) is the individual clearance estimate:
\[CL_i = \theta_{TVCL} \cdot \exp(\eta_i) \tag{1}\]
Calculating this in R yields:
\[CL_i = 0.247 \cdot \exp(0.55194) = 0.42894 \tag{2}\]
Great! We obtained our reference solution for the MAP parameter individualization. We can now visually compare DV, PRED, and IPRED:
# plot DV, PRED, IPRED
nm_out |>
filter(TIME > 0) |>
pivot_longer(cols=c(PRED, IPRED, DV), names_to="variable", values_to="value") |>
ggplot(aes(x=TIME, y=value, group=variable, color=variable))+
geom_point()+
geom_line()+
labs(
y = "Concentration [mg/L]",
x = "Time after last dose [h]",
title = "Comparison of DV, PRED and IPRED for ID 5",
color = "Source"
) +
theme_bw() 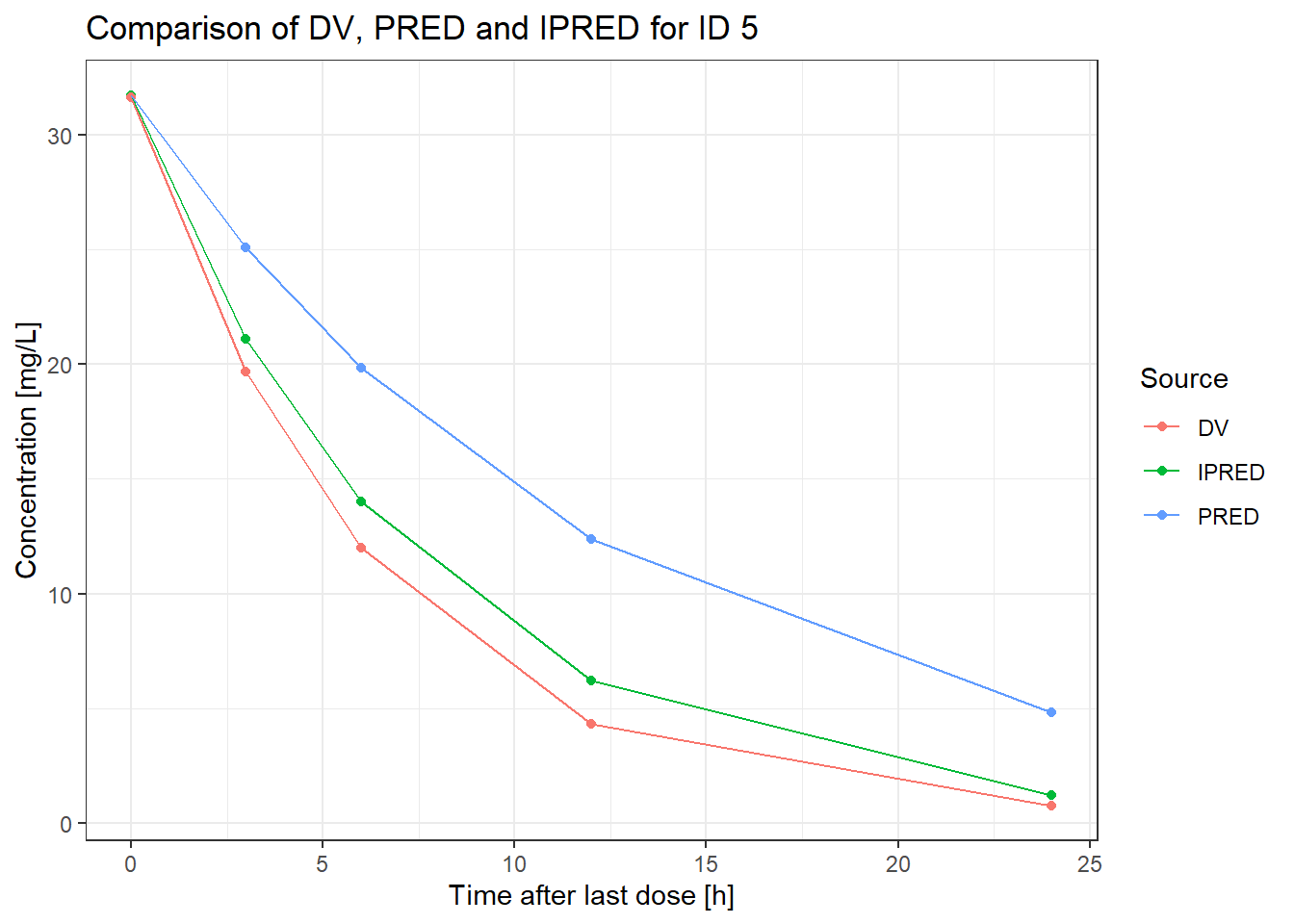
Notably, our reference individual’s data (DV) diverges from typical predictions (PRED), while individualized predictions (IPRED) fall in between. Let’s dive deeper into the process to understand these differences.
As described earlier, the primary goal of a Bayesian approach is to obtain the posterior distribution, either as the mode or as the complete distribution. Bayes’ theorem is commonly presented as follows:
\[P(A|B) = \frac{P(A) \cdot P(B|A)}{P(B)} \tag{3}\]
Here, conditional probabilities are utilized, and \(P(A|B)\) represents the probability of event \(A\) given event \(B\) has occurred. However, this remains quite theoretical. Let’s directly translate it into the context of a pharmacokinetic NLME model.
In pharmacometrics, we aim to determine the most likely individual random effect \(\eta_i\) (which translates to the individual parameter \(CL_i\)), given the observed concentration data \(Y_{i}\) for the individual. Therefore, we are mostly interested to find the posterior distribution of the individual random effect \(\eta_i\) given the data \(Y_{i}\):
\[p(\eta_i|Y_{i}) = \frac{p(\eta_i) \cdot p(Y_{i}|\eta_i)}{p(Y_i)} \tag{4}\]
with
The marginal likelihood \(p(Y_{i})\) is typically neglected because it just acts as a scaling factor, does not depend on \(\eta_i\), and is computationally difficult due to a high-dimensional integral. Thus, the formula is often simplified to:
\[p(\eta_i|Y_{i}) \propto p(\eta_i) \cdot p(Y_{i}|\eta_i) \tag{5}\]
Removing the marginal likelihood gives an unnormalized posterior distribution, indicated by the proportional sign. Working with an unnormalized posterior is acceptable when our when we solely care about finding the mode of the posterior distribution (MAP estimate), as normalization is unnecessary in this scenario. But how exactly do we calculate the MAP estimate?
To find the most likely parameter for an individual, we must identify the maximum of the posterior distribution (MAP estimate). Mathematically, this involves finding the parameter \(\eta_i^*\) that maximizes the posterior:
\[\eta_i^* = \underset{\eta_i}{\mathrm{argmax}}~ p(\eta_i|Y_{i}) = \underset{\eta_i}{\mathrm{argmax}}~ p(\eta_i) \cdot \prod_{j=1}^{m} p(Y_{ij}|\eta_i) \tag{6}\]
Dealing with products of small probability densities can be cumbersome (and mathematically instable), so taking the logarithm simplifies the calculation:
\[\eta_i^* = \underset{\eta_i}{\mathrm{argmax}}~ \log(p(\eta_i|Y_{i})) = \underset{\eta_i}{\mathrm{argmax}}~ \log(p(\eta_i)) + \sum_{j=1}^{m} \log(p(Y_{ij}|\eta_i)) \tag{7}\]
In the end, we would have to use a numerical optimizer function to explore the parameter space of \(\eta_i\) and locate the maximum of the posterior distribution (\(\eta_i^*\)). To fully express the equation, we must define both the log prior \(\log(p(\eta_i))\) and log likelihood \(\log(p(Y_{ij}|\eta_i))\) terms. Let’s explore these in detail.
The prior distribution \(p(\eta_i)\) captures our inital beliefs and uncertainties regarding \(\eta_i\) before observing the data. Bayesian methods allow to incorporate prior knowledge through various distributions and parameters (which is why Bayesians are sometimes being criticized of being too subjective). In pharmacometrics, a common approach is using a prior based on a previously estimated model, typically a normal distribution with mean 0 and variance \(\omega^2_{CL}\) estimated from the NLME model. In contrast to other disciplines, the choice of our priors is generally less controversial, although there has been recent discussion regarding whether this one-approach-fits-all is always appropriate or if priors should be adjusted (e.g., flattened compared to the NLME estimate) in certain situations. See Hughes and Keizer (2021) for more information. The general “role” of the prior term is that strong deviations from the “typical” individual should only be considered when it allows us do substantially better explain the observed data. I like to see it as some kind of penalty function which prevents us from doing a potentially flawed curve fitting exercise. The probability density function (PDF) of a normal distribution can be used to calculate its contribution:
\[p(\eta_i) = \frac{1}{\sqrt{2\pi\omega^2}} \cdot \exp\left(-\frac{(\eta_i-\mu)^2}{2\omega^2}\right) \tag{8}\]
Since \(\mu\) is typically 0, this simplifies to:
\[p(\eta_i) = \frac{1}{\sqrt{2\pi\omega^2}} \cdot \exp\left(-\frac{\eta_i^2}{2\omega^2}\right) \tag{9}\]
Taking the log yields:
\[\log(p(\eta_i)) = -0.5 \log(2\pi\omega^2) - \frac{\eta_i^2}{2\omega^2} \tag{10}\]
Now, we can compute the prior term for any given individual \(\eta_i\), using variance \(\omega^2_{CL}\) (e.g., 0.11) from our NLME model. If we have a good reason to believe that our prior should be different (e.g., we apply our model to another population), we could adjust the variance accordingly (as described in Hughes and Keizer (2021)).
The likelihood term \(p(Y_{ij}|\eta_i)\) is the probability of observing the data point \(Y_{ij}\) given the parameter \(\eta_i\). As we usually assume the residuals of our model predictions to be normally distributed, we again use the normal distribution PDF:
\[p(Y_{ij}|\eta_i) = \frac{1}{\sqrt{2\pi\sigma^2}} \cdot \exp\left(-\frac{(Y_{ij}-f(x_{ij}; \eta_i))^2}{2\sigma^2}\right) \tag{11}\]
where
Taking the log yields:
\[\log(p(Y_{ij}|\eta_i)) = -0.5 \log(2\pi\sigma^2) - \frac{(Y_{ij}-f(x_{ij}; \eta_i))^2}{2\sigma^2} \tag{12}\]
Please note that in our case (a combined additive and proportional RUV model), \(\sigma^2\) represents the combined variances at time \(t_{ij}\) and prediction \(f(x_{ij})\). As the structural solution of our model, \(f(x_{ij})\), is a constant for a given \(t_{ij}\), we can compute the combined variance as
\[\sigma^2 = \sigma^2_{prop} \cdot f(x_{ij})^2 + \sigma^2_{add} \tag{13}\]
Therefore, we later have to calculate the \(\sigma^2\) for each data point \(Y_{ij}\) individually.
Writing out the log prior (Equation 10) and log likelihood (Equation 12) terms in our MAP estimation objective function (Equation 7), we obtain:
\[\eta_i^* = \underset{\eta_i}{\mathrm{argmax}}~\left(\left[-0.5 \log(2\pi\omega^2) - \frac{\eta_i^2}{2\omega^2}\right] ~ + \sum_{j=1}^m \left[-0.5 \log(2\pi\sigma^2) - \frac{(Y_{ij}-f(x_{ij}; \eta_i))^2}{2\sigma^2}\right]\right) \tag{14}\]
This final equation will guide our numerical optimizer (optim function in R) to determine the maximum, providing us with the individual MAP estimate. Let’s implement this method in R and reproduce our NONMEM reference solution!
We start by defining a function to calculate the prior term given by Equation 10. Here, we simply pass the individual \(\eta_i\) and the model parameters (including \(\omega^2_{CL}\)) as input arguments, and the function returns the log probability of the given \(\eta_i\) under the prior distribution:
We can test this function by illustrating the prior term across a range of \(\eta_i\) values:
# define range
eta_i <- seq(-2, 2, 0.01)
# calculate prior term
prior <- prior_fun(eta_i = eta_i, mod_par = mod_par)
# create tibble
prior_tibble <- tibble(
eta_i = eta_i,
p = prior,
source = "prior"
)
# plot prior term
prior_tibble |>
ggplot(aes(x=eta_i, y=exp(p)))+
geom_line(color = "darkblue", linewidth = 0.8)+
geom_vline(xintercept = 0, linetype = "dashed", color = "darkblue", linewidth = 0.6)+
labs(
x = expression(eta[i]),
y = "Probability density",
title = "Prior term (random effect)"
)+
theme_bw()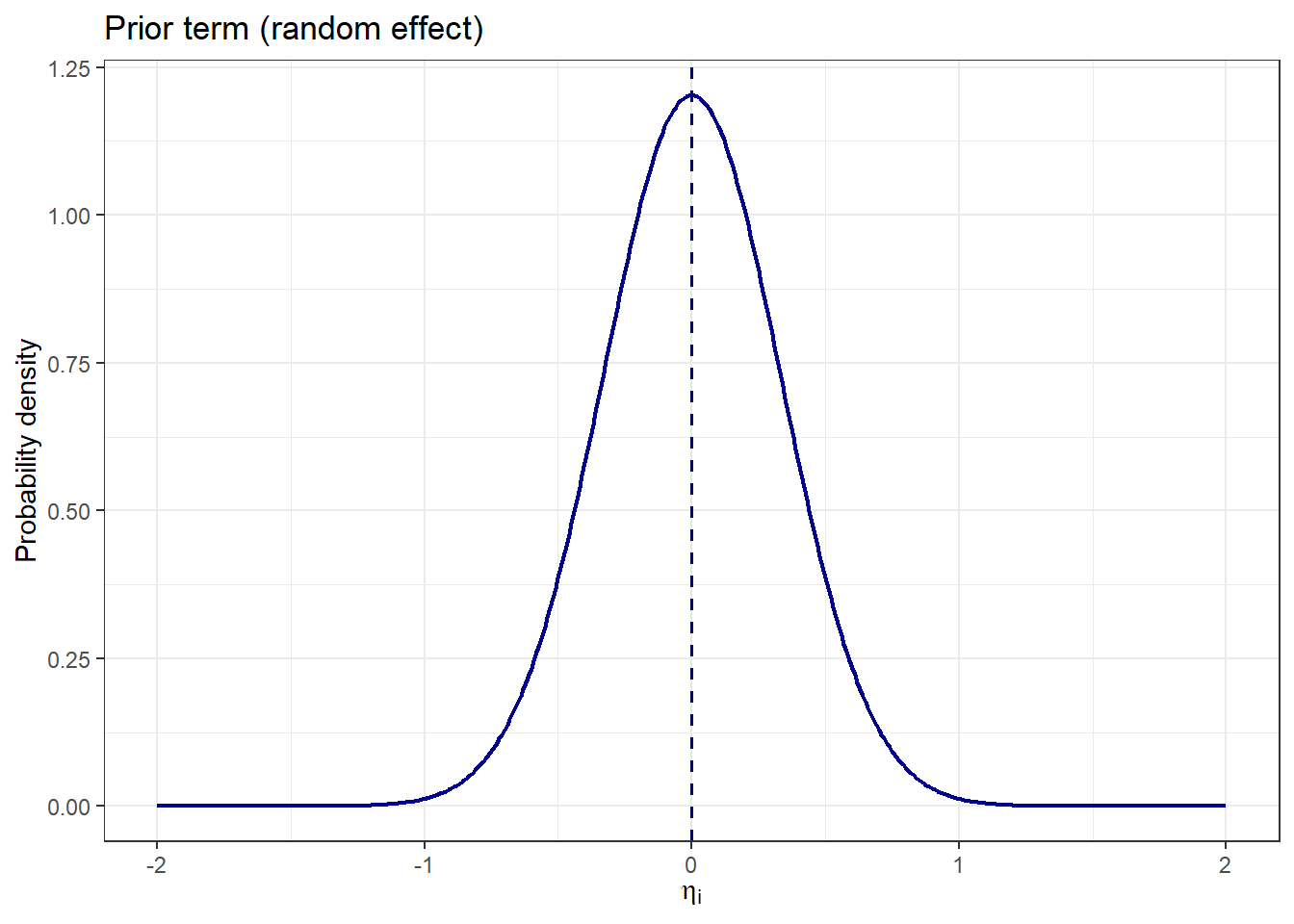
The following plot shows how these \(\eta_i\) values map onto the clearance domain:
# plot prior term
prior_tibble |>
ggplot(aes(x=mod_par$tvcl*exp(eta_i), y=exp(p)))+
geom_line(color = "darkblue", linewidth = 0.8)+
geom_vline(xintercept = mod_par$tvcl, linetype = "dashed", color = "darkblue", linewidth = 0.6)+
labs(
x = expression(CL[i]),
y = "Probability density",
title = "Prior term (clearance)"
)+
theme_bw()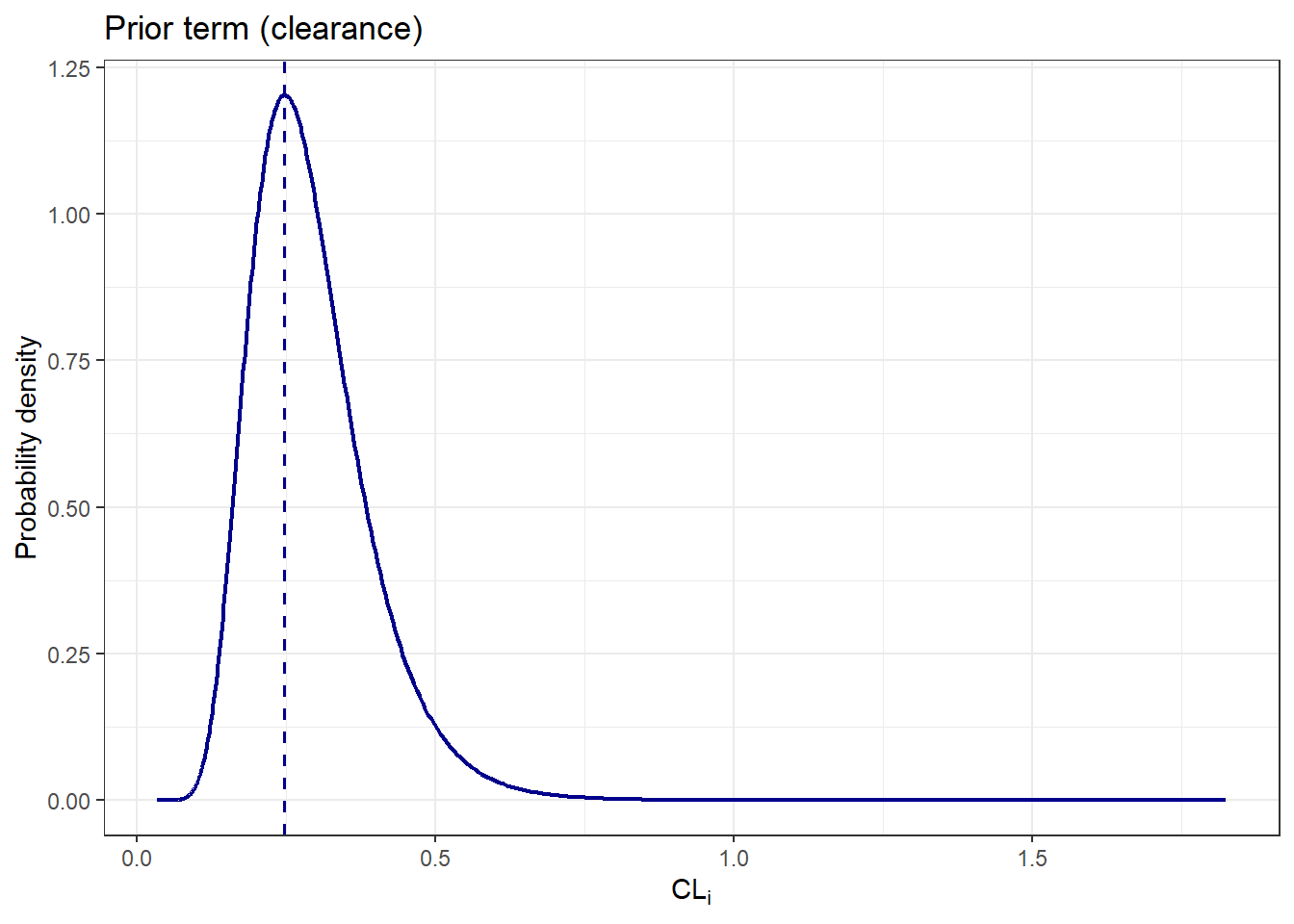
From the plots, we see that certain values of \(\eta_i\) and \(CL_i\) are more likely than others, based on our prior beliefs derived from the NLME model estimates, before observing any individual data. Let’s continue with the likelihood term:
To calculate the log likelihood term described in Equation 12, we first have to define a model prediction function. Given our simple one-compartment model, we use a closed-form expression, though the principles apply equally to ODE-based models. More details on the model prediction function can be found in the previous blogpost, see Klose (2025).
Next, we construct the likelihood function for individual observations. Please note that we have to calculate the \(\sigma^2\) for each data point \(Y_{ij}\) individually, as the variance contains an element proportional to the model prediction \(f_i\) (see Equation 12). The following equation calculates the log likelihood for a single observation:
function: log_likelihood_fun_single()
# define likelihood function for a single observation
log_likelihood_fun_single <- function(eta_i, dose, vd, theta_tvcl, t_ij, Y_ij, sigma2_add, sigma2_prop){
# get model predictions
f_ij <- model_fun(eta_i, dose, vd, theta_tvcl, t_ij)
# calculate resulting sigma2 for each timepoint (prop variance is scaled based on f_i^2)
sigma2 <- sigma2_prop * f_ij^2 + sigma2_add
# calculate probability
log_lik <- - 0.5 * log(2*pi*sigma2) - (Y_ij - f_ij)^2/(2*sigma2)
# return log likelihood
return(log_lik)
}To illustrate this, we calculate the likelihood for each observation, then sum these to obtain the total likelihood for a given \(\eta_i\). We demonstrate this using an example with \(\eta_i = 0\):
# calculate lok lik per row
sim_data_id5 <- sim_data_id5 |>
rowwise() |>
mutate(
log_lik = case_when(
EVID == 0 ~ log_likelihood_fun_single(
eta_i = 0,
dose = mod_par$dose,
vd = mod_par$tvvd,
theta_tvcl = mod_par$tvcl,
t_ij = TIME,
Y_ij = DV,
sigma2_add = mod_par$sigma2_add,
sigma2_prop = mod_par$sigma2_prop
),
EVID == 1 ~ NA_real_
)
) |>
ungroup() |>
mutate(
sum_log_lik = sum(log_lik, na.rm = TRUE)
)
# show sim_data_id5
sim_data_id5 |>
kable() |>
kable_styling()| ID | TIME | EVID | AMT | RATE | DV | MDV | log_lik | sum_log_lik |
|---|---|---|---|---|---|---|---|---|
| 5 | 0.00 | 1 | 100 | 0 | 0.00000 | 1 | NA | -17.93624 |
| 5 | 0.01 | 0 | 0 | 0 | 31.61900 | 0 | -4.031343 | -17.93624 |
| 5 | 3.00 | 0 | 0 | 0 | 19.66000 | 0 | -3.844624 | -17.93624 |
| 5 | 6.00 | 0 | 0 | 0 | 12.00700 | 0 | -3.718827 | -17.93624 |
| 5 | 12.00 | 0 | 0 | 0 | 4.33360 | 0 | -3.514076 | -17.93624 |
| 5 | 24.00 | 0 | 0 | 0 | 0.78148 | 0 | -2.827369 | -17.93624 |
We observe individual likelihood contributions and their sum. To streamline this process, we define a function that computes the summed likelihood across multiple observations:
function: log_likelihood_fun_multiple()
# define likelihood function for a set of observations
log_likelihood_fun_multiple <- function(df, eta_i, mod_par){
# retrieve information from mod_par
dose <- mod_par$dose
vd <- mod_par$tvvd
theta_tvcl <- mod_par$tvcl
sigma2_add <- mod_par$sigma2_add
sigma2_prop <- mod_par$sigma2_prop
# calculate log lik per row
log_lik_sum <- df |>
rowwise() |>
mutate(
log_lik = case_when(
EVID == 0 ~ log_likelihood_fun_single(
eta_i = eta_i,
dose = dose,
vd = vd,
theta_tvcl = theta_tvcl,
t_ij = TIME,
Y_ij = DV,
sigma2_add = sigma2_add,
sigma2_prop = sigma2_prop
),
EVID == 1 ~ NA_real_
)
) |>
ungroup() |>
pull(log_lik) |>
sum(na.rm = TRUE)
# return log likelihood sum
return(log_lik_sum)
}Testing this function quickly confirms consistency of the obtained summed up likelihood with the previous result from the table (see above):
[1] -17.93624Now, we can visualize the likelihood term across a range of \(\eta_i\) values, similar to what we have did for the prior term:
# define range
eta_i <- seq(-2, 2, 0.01)
# empty list
ll_list <- list()
# loop over each element of eta_i
for(cur_eta_i in eta_i){
# calculate likelihood term
ll_list[[as.character(cur_eta_i)]] <- log_likelihood_fun_multiple(
df = sim_data_id5,
eta_i = cur_eta_i,
mod_par = mod_par
)
}
# convert to vector
ll_vector <- ll_list |> unlist() |> unname()
# create tibble
likelihood_tibble <- tibble(
eta_i = eta_i,
p = ll_vector,
source = "likelihood"
)
# plot likelihood term
likelihood_tibble |>
ggplot(aes(x=eta_i, y=exp(p)))+
geom_line(color = "darkred", linewidth = 0.8)+
geom_vline(xintercept = eta_i[which.max(ll_vector)], linetype = "dashed", color = "darkred", linewidth = 0.8)+
labs(
x = expression(eta[i]),
y = "Likelihood",
title = "Likelihood term"
)+
theme_bw()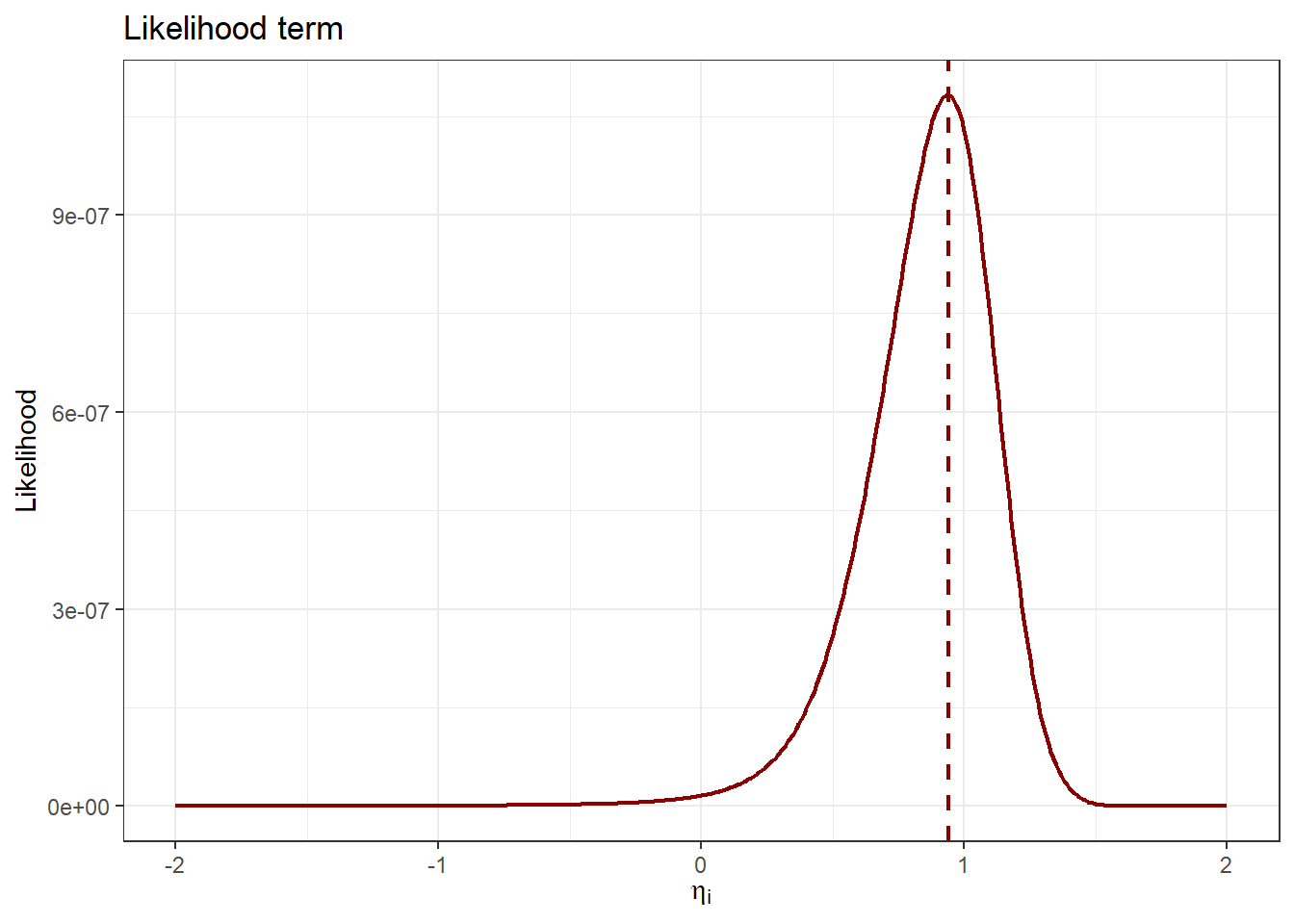
The likelihood plot clearly indicates which \(\eta_i\) values best describe the observed data. Identifying the maximum likelihood \(\eta_i\) is straightforward:
[1] 0.94The optimal \(\eta_i\) value according to the likelihood term (and ignoring any prior information) is 0.94. Please note: As the likelihood is the product of many probabilities, each between 0 and 1, we typically deal with extremely small numerical values. Therefore, it is common practice to use logarithmic transformations for numerical stability. Next, we combine the prior and likelihood terms to perform MAP estimation.
We now have to define an objective function for numerical optimization, combining prior and likelihood terms to estimate the posterior (as shown in Equation 14).
function: map_obj_fun()
# define MAP estimation objective function
map_obj_fun <- function(eta_i, df, mod_par){
# calculate log prior term
log_prior <- prior_fun(
eta_i = eta_i,
mod_par = mod_par
)
# calculate log likelihood term
log_likelihood <- log_likelihood_fun_multiple(
df = df,
eta_i = eta_i,
mod_par = mod_par
)
# combine both
log_posterior <- log_prior + log_likelihood
# return negative log posterior
return(-log_posterior)
}Please note that we are returning the negative log posterior as it is easier to minimize a function than to maximize it. Using R’s optim function, we estimate the MAP numerically. Here is the output form the optim call:
$par
[1] 0.5519271
$value
[1] 16.08691
$counts
function gradient
13 7
$convergence
[1] 0
$message
NULLThe resulting MAP estimate for \(\eta_i\) is 0.5519271, closely matching the reference solution (0.55194) with an acceptable difference (-0.0000128887). Similarly to the other terms, we can visualize the posterior term across a range of \(\eta_i\) values:
# define range
eta_i <- seq(-2, 2, 0.01)
# empty list
post_list <- list()
# loop over each element of eta_i
for(cur_eta_i in eta_i){
# calculate likelihood term
post_list[[as.character(cur_eta_i)]] <- map_obj_fun(
eta_i = cur_eta_i,
df = sim_data_id5,
mod_par = mod_par
)
}
# convert to vector
post_vector <- post_list |> unlist() |> unname()
# create tibble
posterior_tibble <- tibble(
eta_i = eta_i,
p = -post_vector,
source = "posterior"
)
# plot likelihood term
posterior_tibble |>
ggplot(aes(x=eta_i, y=exp(p)))+
geom_line(color = "darkgreen", linewidth = 0.8)+
geom_vline(xintercept = map_est$par, linetype = "dashed", color = "darkgreen", linewidth = 0.8)+
labs(
x = expression(eta[i]),
y = "Unnormalized posterior density",
title = "Posterior distribution"
)+
theme_bw()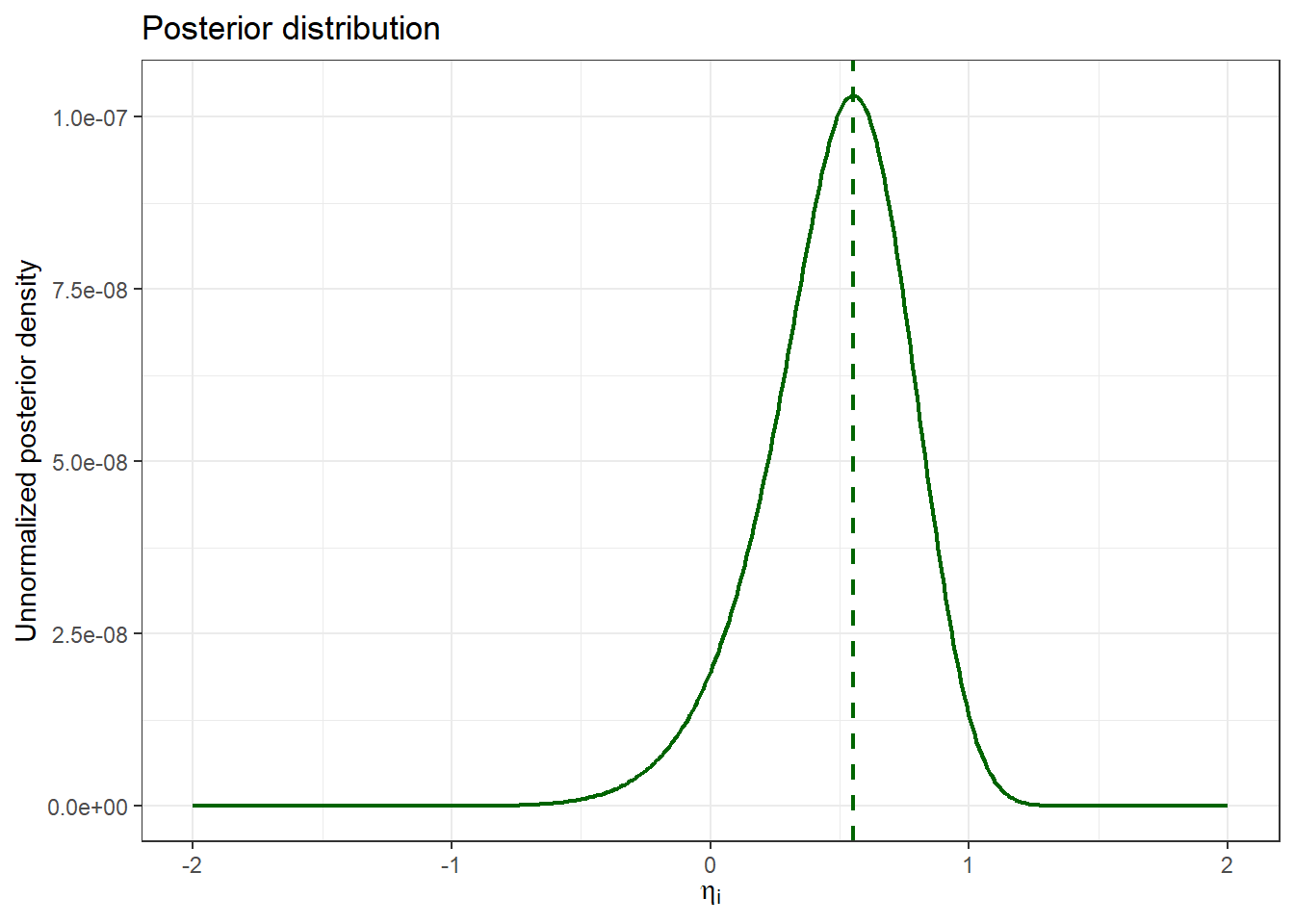
Finally, we compare the MAP estimate (mode of the posterior) with prior and likelihood terms visually:
# combine likelihood and prior
comp_tibble <- rbind(
prior_tibble,
likelihood_tibble,
posterior_tibble
) |>
mutate(source = factor(source, levels = c("prior", "posterior", "likelihood")))
# define linewidth
linewidth <- 0.8
# plot both distributions with different colors and fill
comp_tibble |>
ggplot(aes(x=eta_i, y=exp(p), fill = source, color = source))+
scale_x_continuous(breaks = c(-2,-1,0, signif(map_est$par,2), signif(eta_i_max_likelihood,2), 2))+
geom_line(linewidth = linewidth)+
geom_vline(
data = data.frame(source = factor("prior", levels = c("prior", "posterior", "likelihood"))),
aes(xintercept = 0),
color = "darkblue", linetype = "dashed", linewidth = linewidth
) +
geom_vline(
data = data.frame(source = factor("posterior", levels = c("prior", "posterior", "likelihood"))),
aes(xintercept = map_est$par),
color = "darkgreen", linetype = "dashed", linewidth = linewidth
) +
geom_vline(
data = data.frame(source = factor("likelihood", levels = c("prior", "posterior", "likelihood"))),
aes(xintercept = eta_i_max_likelihood),
color = "darkred", linetype = "dashed", linewidth = linewidth
) +
scale_color_manual(values = c(prior = "darkblue",
posterior = "darkgreen",
likelihood = "darkred")) +
facet_wrap(~source, scales = "free", ncol = 1)+
labs(
x = expression(eta[i]),
y = "(Unnormalized) probability density",
title = "Comparison of prior, likelihood, and posterior",
color = "Source"
) +
theme_bw() +
theme(legend.position = "none")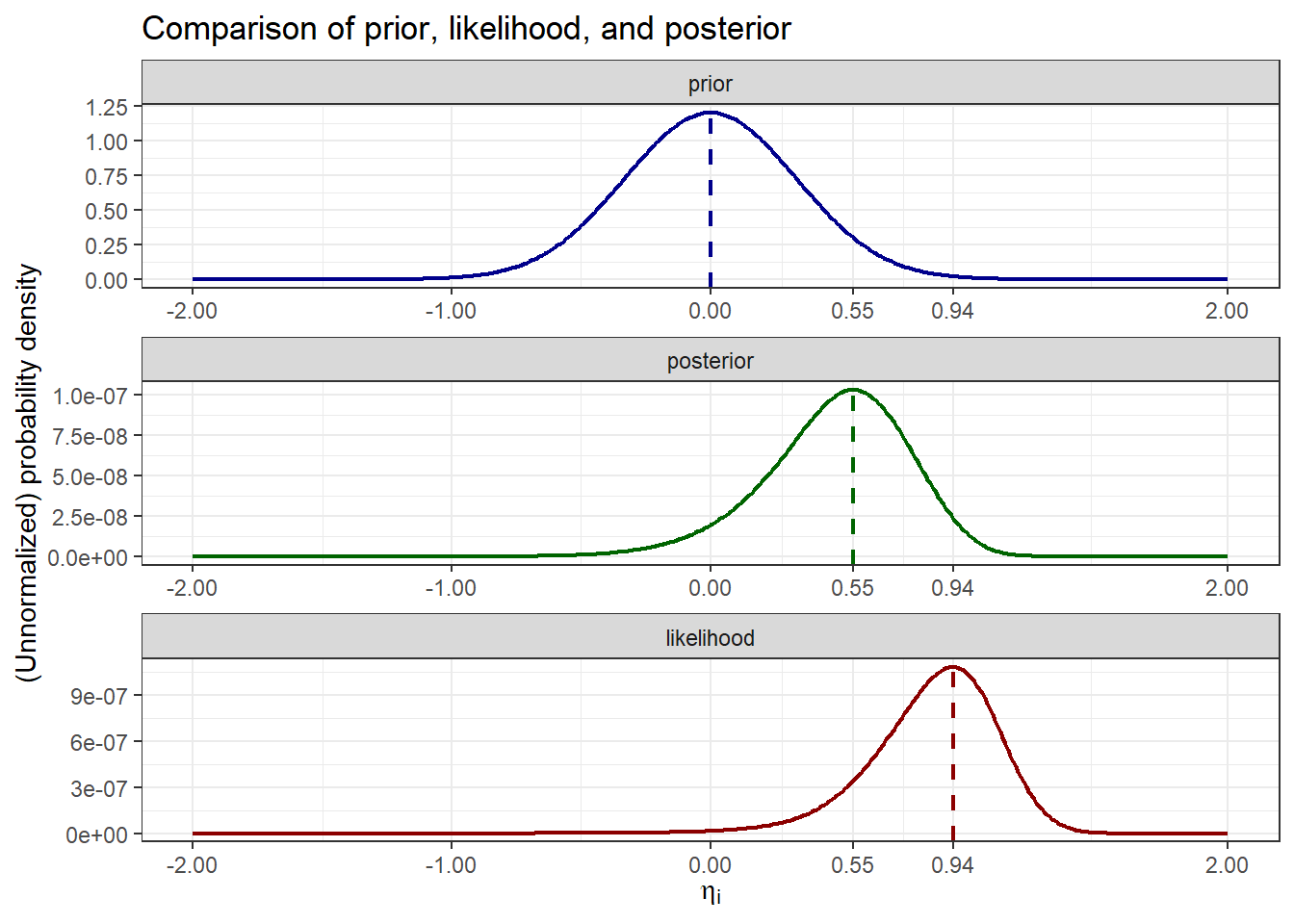
This clearly demonstrates how the posterior is influenced by both the prior and the likelihood, with the MAP estimate (mode of the posterior, green dashed line) reflecting a balance between these two sources of information.
This simple example illustrates how to estimate the individual parameter \(\eta_i\) (which translates to an individual clearance \(CL_i\)) for a single subject using a Bayesian approach. We have seen that the posterior distribution, often summarized by its mode (the MAP or EBE estimate), represents a compromise between the prior and the likelihood. This powerful technique enables the continuous integration of prior knowledge with new data and is very useful for many pharmacometric workflows. With that, I conclude this blog post and hope you enjoyed it. If you have any questions or feedback, please feel free to leave a comment.
MAP estimates are also known as Empirical Bayes Estimates (EBE).↩︎
Depending on the estimation algorithm.↩︎
The dense sampling in combination with a simple additive error model for RUV led to a scenario where the posterior was nearly equal to the likelihood. Therefore, I have increased the additive error and introduced a proportional term as well. This places the posterior in the middle and I can recycle the old dataset I have simulated before.↩︎
Actually, this took me quite some time to figure out. I was using the model from the previous blogpost, which only had an additive error and was missing the INTERACTION option (which doesn’t matter if you are just using a constant additive error). With the newly introduced proportional error, I then had a mismatch between my calculations and the reference and I couldn’t figure out why. The missing INTERACTION was the solution, as with the introduction of the proportional error the RUV does not remain constant (which NONMEM is assuming when INTERACTION is missing). Lesson learned!↩︎
@online{klose2025,
author = {Klose, Marian},
title = {Reproducing {NONMEM’s} {MAP} Estimation in {R}},
date = {2025-03-31},
url = {https://marian-klose.com/posts/bayes_map_estimation_in_r/index.html},
langid = {en}
}
---
title: "Reproducing NONMEM's MAP estimation in R"
description: "How to perform Bayesian MAP estimation yourself using R and why you should care. "
author:
- name: Marian Klose
url: https://github.com/marianklose
orcid: 0009-0005-1706-6289
date: 03-31-2025 # MM-DD-YYYY
categories: [NONMEM, Bayes, MAP, EBE, Estimation]
image: preview.gif
draft: false
echo: true
execute:
freeze: true # never re-render during project render (dependencies might change over time)
echo: true
message: false
warning: false
citation:
url: https://marian-klose.com/posts/bayes_map_estimation_in_r/index.html
format:
html:
number-sections: true
toc: true
code-fold: true
code-tools: true
---
```{r}
# load packages
library(dplyr)
library(ggplot2)
library(readr)
library(kableExtra)
library(xpose4)
library(tidyr)
```
# Motivation {#sec-motivation}
Bayesian estimation is a widely-used method in pharmacometrics. Many pharmacometricians utilize individual predictions (`IPRED`) in their diagnostics, which represent simulations based on the *maximum a-posteriori* (MAP) estimates [^1]. These estimates essentially represent the mode of the so-called *posterior* distribution, which combines prior knowledge about the population and new evidence about the particular individual at hand (more to that later). `MAP` estimates also play a crucial role in *Model-Informed Precision Dosing* (MIPD), where one aims to predict the concentration-time profile of an individual, given a pharmacokinetic NLME model and a set of drug concentrations measured through a *Therapeutic Drug Monitoring* (TDM) program. During model building, the underlying individualized `ETAs` are often used for covariate screening, provided that shrinkage permits it. As you can see, Bayesian estimation is quite prominent in pharmacometric workflows. Thomas Bayes would be proud of us!
{width=40% #fig-thomas-bayes}
In many scenarios, these Bayesian calculations happen automatically *under the hood* when fitting pharmacometric models (e.g., in NONMEM), making it quite easy to use Bayesian estimates without exploring the underlying concepts and calculations. I myself did this for quite some time. Reproducing calculations through equations is often the best way to grasp the underlying principles. Therefore, I have decided to write this blogpost, in which I want to explain the Bayesian idea and reproduce a simple Bayesian MAP estimation in R. I will mainly focus on the point estimates of the posterior distribution (`MAP` or `EBE`). Addressing the full *posterior* distribution is also important and might be covered in a future post. There are other nice blogposts which cover full Bayesian approaches in more detail, such as @navarro2023.
Please note: These are just my personal reflections and interpretations of Bayesian concepts. I cannot guarantee that my explanations, equations, or terminology are flawless. If you notice any inaccuracies, please let me know so I can correct them!
# Structure {#sec-structure}
Let me briefly outline how I structured this blogpost. The overall goal is to better understand the Bayesian concept behind MAP estimation and to derive an individualized clearance estimate for a virtual patient using R, step by step.
I start with my own little introduction of the Bayesian idea (@sec-bayesian-idea) using a real-world example and define the key components—prior, likelihood, and posterior.
This is then followed by a pharmacometric example using a simulated dataset (from my previous blogpost) and a simple one-compartment i.v. bolus PK model as reference (@sec-pharmex). This section also includes our NONMEM reference solution which is later used to validate our calculations in R.
Next, we try to explore the Bayesian theory a bit more, dealing with the mathematical formulation of MAP estimation and explaining how the prior and likelihood combine to form the posterior (@sec-bayesth).
Afterwards, we move on to the R-based MAP reproduction (@sec-rrepro). We implement the prior and likelihood functions, combine them into an optimization routine, and estimate the individual parameter from scratch. Finally, we are able to compare the R-based result to the NONMEM output and visualize how prior, likelihood, and posterior interact.
With that being said, let's get started!
# The Bayesian Idea: Updating Beliefs {#sec-bayesian-idea}
## Starting with an example {#sec-bayesian-idea-example}
I would say that many of us naturally think Bayesian, even if we are not aware of it or if we don't label it that way. At its core, Bayesian statistics is about updating your beliefs once new data or information becomes available. Let’s consider an example from the real-world to illustrate this idea.
Imagine you drive to work every day. If someone would ask you "How long will it take you to get to work tomorrow?", you would probably have a good idea, simply based on your past experiences. 30 minutes might be your best guess, but would you bet money that it will be exactly 30 minutes? Probably not, as you will always have some uncertainty associated with it. Perhaps something between 20 and 40 minutes would be reasonable based on your previous trips. Now, let's assume you get into your car the next morning and after 25 minutes, you have made it halfway.
{width=80% #fig-traffic-jam}
Would you stick to your initial belief that it will take you 30 minutes? Probably not, you would likely revise it (or try to break all speed limits). But would you simply double the 25 minutes to predict a 50-minute commute? This is also unlikely, given your experience suggesting that 40 minutes is usually the upper limit. So, maybe you would adjust your estimate to 38 minutes, assuming that the traffic will get better soon. This is Bayesian thinking in action: Updating your beliefs with new data. But so far without any equation and rather based on gut-feeling.
## Terminology {#sec-bayesian-idea-terminology}
Now, let’s map this real-world scenario to some Bayesian terminology. There are three key components in every Bayesian analysis:
- **Prior:** Your initial belief - 30 minutes, plus some uncertainty.
- **Likelihood:** The new data - taking 25 min to cover half the distance and suggesting 50 min for the full trip.
- **Posterior:** Your updated estimate - now around 38 minutes, combining prior and likelihood.
Bayesian analysis starts with a prior, which you revise using new data (likelihood) to obtain the posterior. In pharmacometrics, we often encounter two levels of complexity when it comes to Bayes:
- **MAP / EBE:** Simply focuses on the mode of the posterior distribution and ignores its uncertainty.
- **Full Bayesian:** Considers the entire posterior distribution, not just the mode or a point estimate.
Many pharmacometricians use MAP estimates due to their computational simplicity and their direct integration into standard NLME routines, while full Bayesian methods offer a more comprehensive view by integrating uncertainty even after new data became available. Full Bayesian methods are more and more used in the field, also thanks to some nice tutorials by @margossianFlexibleEfficientBayesian2022 for Stan/Torsten and by @johnstonBayesianEstimationNONMEM2024 for NONMEM itself, both from the Metrum Research Group.
## Our goal in pharmacometrics {#sec-bayesian-idea-goal}
So, what role does Bayesian methodology play in pharmacometrics? Obviously it is not about optimizing your commute. Instead, we typically use Bayesian estimation to individualize the model parameters for a given individual $i$, which has a set of unique observations $Y_{i}$. This concept was first introduced to the pharmacometric community by @sheiner1972, if I am not mistaken. On the one hand, `MAP` estimation happens during model building, at each iteration step [^2] and then after the actual estimation has finished, at the `POSTHOC` step. On the other hand, it is also used in MIPD settings as described above. The approach remains the same, and we will later have a look at a simple pharmacokinetic example to illustrate this.
So far we used a relatable example rather focusing on the intuition behind Bayesian thinking. Now we want to dive a bit into the mathematics behind it to be able to formally reproduce a simple Bayesian MAP estimation in R.
# Pharmacometric example and reference solution {#sec-pharmex}
## Data and visualization {#sec-pharmex-data}
Without data, no Bayesian parameter individualization. For our MAP estimation, we are using the same simulated data set I have defined in the previous blogpost about NLME modelling. See @klose2025 for more details about this data set. Let's start by loading the simulated concentration-time data and showing the head of the data set:
```{r}
# read in simulated dataset from previous blogpost
sim_data <- read_csv("./data/sim_data.csv")
# show data
sim_data |>
head() |>
kable() |>
kable_styling()
```
We will focus on ID 5, which has lower simulated concentrations than the average individual, making it easier to observe differences between typical and individualized profiles. Here's a plot to visualize these concentration-time profiles of ID 5 and the other IDs of the virtual population:
```{r}
#| label: fig-sim-vis
#| fig-cap: "Simulated concentration-time profiles for 10 individuals after i.v. bolus injection. ID 5 (blue) represents our exemplary ID."
# show individual profiles
sim_data |>
filter(EVID == 0) |>
mutate(flag = if_else(ID == 5, "Reference", "Others")) |>
ggplot(aes(x=TIME, y=DV, group=ID, color=as.factor(flag))) +
geom_point()+
geom_line()+
theme_bw()+
scale_y_continuous(limits=c(0,NA))+
labs(x="Time after last dose [h]", y="Concentration [mg/L]")+
scale_color_manual("Individual", values=c("grey", "darkblue"))+
ggtitle("Simulated concentration time data after i.v. bolus injection")
```
We will later need this data set when running the NONMEM-based MAP estimation, so we have to save it to file. Prior to that, we will filter the data set to only include the data for ID 5:
```{r}
# define sim_data with ID == 5
sim_data_id5 <- sim_data |>
filter(ID == 5)
# save data for NONMEM
sim_data_id5 |>
write_csv("./data/sim_data_ID5.csv")
```
With that being done, we are all set to define the NLME model in NONMEM in a next step!
## NLME model structure {#sec-pharmex-nlme}
For our example and reference, we'll use a simple one-compartment IV model with first-order kinetics, previously fitted to similar data (@klose2025). Here's a sketch of the simple model structure:
{width=100% #fig-mod-struct}
Assuming our model is already fitted, our goal is to individualize parameters for ID 5. The model parameter estimates are based on the fitted model from the previous blogpost and are as follows:
- $CL$ = 0.247 L/h
- $V$ = 3.15 L
- $\omega^2_{CL}$ = 0.11
- $\sigma^2_{RUV\_ADD}$ = 2.00
- $\sigma^2_{RUV\_PROP}$ = 0.50
In a next step, we will translate this into a NONMEM model. Note that we added a proportional error term to the previously used model to better illustrate the differences among prior, likelihood, and posterior distributions [^3]. For the same reason, we increased the additive error to 2 mg/L. Let's store this information, along with the 100 mg intravenous bolus dose administered to the individual, in a list object for easy retrieval during subsequent calculations:
```{r}
# store model parameters in list
mod_par <- list(
tvcl = 0.247,
tvvd = 3.15,
omega2_CL = 0.11,
sigma2_add = 2,
sigma2_prop = 0.50,
dose = 100
)
# show
mod_par
```
Great! Now we can go ahead and define the NONMEM model.
## NONMEM model {#sec-pharmex-model}
We have updated our NONMEM model slightly from the last blogpost:
```{.r filename="1cmt_iv_map_est.mod"}
$PROBLEM 1cmt_iv_map_est
$INPUT ID TIME EVID AMT RATE DV MDV
$DATA C:\Users\mklose\Desktop\GitHub\personal-website\posts\bayes_map_estimation_r\data\sim_data_ID5.csv IGNORE=@
$SUBROUTINES ADVAN1 TRANS2
$PK
; define fixed effects parameters
CL = THETA(1) * EXP(ETA(1))
V = THETA(2)
; scaling
S1=V
$THETA
0.247 FIX ; 1 TVCL
3.15 FIX ; 2 TVV
$OMEGA
0.11 FIX ; 1 OM_CL
$SIGMA
0.50 FIX ; 1 SIG_PROP
2.00 FIX ; 2 SIG_ADD
$ERROR
; add residual unexplained variability
IPRED = F
Y = IPRED + IPRED * EPS(1) + EPS(2)
$ESTIMATION METHOD=1 INTERACTION MAXEVAL=0 SIGDIG=3 PRINT=1 NOABORT POSTHOC
$TABLE ID TIME EVID AMT RATE DV PRED IPRED MDV ETA1 CL NOAPPEND ONEHEADER NOPRINT FILE=map_estim_out
```
We have fixed the initial parameter estimates to the final estimates from before and incorporated a combined error model (as described above). By using `MAXEVAL=0`, we avoid any population parameter estimation and the model is simply being evaluated. The `POSTHOC` option computes individual MAP estimates as this is the core of our task. We need to make sure that we include the `INTERACTION` option in the `$ESTIMATION` block, as this tells NONMEM to include the effect of `ETA` on the residual error when performing MAP estimation [^4]. This is important as our error model now depends on `IPRED`, which in turn depends on `ETA.`
After running the model, we'll read the output through `map_estim_out`:
```{r}
# load simulated data
nm_out <- read_nm_table("./models/map_estim_out")
# show simulated data
nm_out |>
head() |>
kable() |>
kable_styling()
```
The `ETA1` (= $\eta_i$) value represents the individual random effect, while `CL` (= $CL_i$) is the individual clearance estimate:
$$CL_i = \theta_{TVCL} \cdot \exp(\eta_i)$$ {#eq-cl-individual}
Calculating this in R yields:
$$CL_i = 0.247 \cdot \exp(0.55194) = 0.42894$$ {#eq-cl-individual-num}
```{r}
#| code-fold: FALSE
# calculate individual MAP estimate
mod_par$tvcl*exp(nm_out$ETA1 |> unique())
```
Great! We obtained our reference solution for the MAP parameter individualization. We can now visually compare `DV`, `PRED`, and `IPRED`:
```{r}
#| label: fig-comp-dv-pred-ipred
#| fig-cap: "Comparison of observations (DV), population predictions (PRED), and individualized predictions based on the MAP estimate for CL (IPRED)."
# plot DV, PRED, IPRED
nm_out |>
filter(TIME > 0) |>
pivot_longer(cols=c(PRED, IPRED, DV), names_to="variable", values_to="value") |>
ggplot(aes(x=TIME, y=value, group=variable, color=variable))+
geom_point()+
geom_line()+
labs(
y = "Concentration [mg/L]",
x = "Time after last dose [h]",
title = "Comparison of DV, PRED and IPRED for ID 5",
color = "Source"
) +
theme_bw()
```
Notably, our reference individual's data (`DV`) diverges from typical predictions (`PRED`), while individualized predictions (`IPRED`) fall in between. Let's dive deeper into the process to understand these differences.
# Bayesian Theory {#sec-bayesth}
## General form of Bayes' theorem {#sec-bayesth-general}
As described earlier, the primary goal of a Bayesian approach is to obtain the posterior distribution, either as the mode or as the complete distribution. Bayes' theorem is commonly presented as follows:
$$P(A|B) = \frac{P(A) \cdot P(B|A)}{P(B)}$$ {#eq-bayes-general}
Here, conditional probabilities are utilized, and $P(A|B)$ represents the probability of event $A$ given event $B$ has occurred. However, this remains quite theoretical. Let's directly translate it into the context of a pharmacokinetic NLME model.
## Pharmacometric context {#sec-bayesth-pharmetrx}
In pharmacometrics, we aim to determine the most likely individual random effect $\eta_i$ (which translates to the individual parameter $CL_i$), given the observed concentration data $Y_{i}$ for the individual. Therefore, we are mostly interested to find the posterior distribution of the individual random effect $\eta_i$ given the data $Y_{i}$:
$$p(\eta_i|Y_{i}) = \frac{p(\eta_i) \cdot p(Y_{i}|\eta_i)}{p(Y_i)}$$ {#eq-bayes-specific-norm}
with
- $p(\eta_i|Y_{i})$: posterior distribution of parameter $\eta_i$ given the individual data $Y_{i}$
- $p(\eta_i)$: prior distribution of parameter $\eta_i$
- $p(Y_{i}|\eta_i)$: likelihood of observing data $Y_{i}$ given parameter $\eta_i$
- $p(Y_{i})$: marginal likelihood of data $Y_{i}$
The marginal likelihood $p(Y_{i})$ is typically neglected because it just acts as a scaling factor, does not depend on $\eta_i$, and is computationally difficult due to a high-dimensional integral. Thus, the formula is often simplified to:
$$p(\eta_i|Y_{i}) \propto p(\eta_i) \cdot p(Y_{i}|\eta_i)$$ {#eq-bayes-specific-unnorm}
Removing the marginal likelihood gives an unnormalized posterior distribution, indicated by the proportional sign. Working with an unnormalized posterior is acceptable when our when we solely care about finding the mode of the posterior distribution (MAP estimate), as normalization is unnecessary in this scenario. But how exactly do we calculate the MAP estimate?
## MAP estimation {#sec-bayesth-map}
To find the most likely parameter for an individual, we must identify the maximum of the posterior distribution (MAP estimate). Mathematically, this involves finding the parameter $\eta_i^*$ that maximizes the posterior:
$$\eta_i^* = \underset{\eta_i}{\mathrm{argmax}}~ p(\eta_i|Y_{i}) = \underset{\eta_i}{\mathrm{argmax}}~ p(\eta_i) \cdot \prod_{j=1}^{m} p(Y_{ij}|\eta_i)$$ {#eq-map-norm}
Dealing with products of small probability densities can be cumbersome (and mathematically instable), so taking the logarithm simplifies the calculation:
$$\eta_i^* = \underset{\eta_i}{\mathrm{argmax}}~ \log(p(\eta_i|Y_{i})) = \underset{\eta_i}{\mathrm{argmax}}~ \log(p(\eta_i)) + \sum_{j=1}^{m} \log(p(Y_{ij}|\eta_i))$$ {#eq-map-log}
In the end, we would have to use a numerical optimizer function to explore the parameter space of $\eta_i$ and locate the maximum of the posterior distribution ($\eta_i^*$). To fully express the equation, we must define both the log prior $\log(p(\eta_i))$ and log likelihood $\log(p(Y_{ij}|\eta_i))$ terms. Let's explore these in detail.
### Prior term {#sec-bayesth-map-prior}
The prior distribution $p(\eta_i)$ captures our inital beliefs and uncertainties regarding $\eta_i$ before observing the data. Bayesian methods allow to incorporate prior knowledge through various distributions and parameters (which is why Bayesians are sometimes being criticized of being too subjective). In pharmacometrics, a common approach is using a prior based on a previously estimated model, typically a normal distribution with mean 0 and variance $\omega^2_{CL}$ estimated from the NLME model. In contrast to other disciplines, the choice of our priors is generally less controversial, although there has been recent discussion regarding whether this one-approach-fits-all is always appropriate or if priors should be adjusted (e.g., flattened compared to the NLME estimate) in certain situations. See @hughes2021 for more information. The general "role" of the prior term is that strong deviations from the "typical" individual should only be considered when it allows us do substantially better explain the observed data. I like to see it as some kind of penalty function which prevents us from doing a potentially flawed curve fitting exercise. The probability density function (PDF) of a normal distribution can be used to calculate its contribution:
$$p(\eta_i) = \frac{1}{\sqrt{2\pi\omega^2}} \cdot \exp\left(-\frac{(\eta_i-\mu)^2}{2\omega^2}\right)$$ {#eq-prior-1}
Since $\mu$ is typically 0, this simplifies to:
$$p(\eta_i) = \frac{1}{\sqrt{2\pi\omega^2}} \cdot \exp\left(-\frac{\eta_i^2}{2\omega^2}\right)$$ {#eq-prior-2}
Taking the log yields:
$$\log(p(\eta_i)) = -0.5 \log(2\pi\omega^2) - \frac{\eta_i^2}{2\omega^2}$$ {#eq-prior-3}
Now, we can compute the prior term for any given individual $\eta_i$, using variance $\omega^2_{CL}$ (e.g., 0.11) from our NLME model. If we have a good reason to believe that our prior should be different (e.g., we apply our model to another population), we could adjust the variance accordingly (as described in @hughes2021).
### Likelihood term {#sec-bayesth-map-likelihood}
The likelihood term $p(Y_{ij}|\eta_i)$ is the probability of observing the data point $Y_{ij}$ given the parameter $\eta_i$. As we usually assume the residuals of our model predictions to be normally distributed, we again use the normal distribution PDF:
$$p(Y_{ij}|\eta_i) = \frac{1}{\sqrt{2\pi\sigma^2}} \cdot \exp\left(-\frac{(Y_{ij}-f(x_{ij}; \eta_i))^2}{2\sigma^2}\right)$$ {#eq-likelihood-1}
where
- $Y_{ij}$: observed data point for individual $i$ at time $j$
- $f(x_{ij}; \eta_i)$: model prediction for individual $i$ at time $j$, given parameter $\eta_i$
- $\sigma^2$: variance representing residual unexplained variability (RUV)
Taking the log yields:
$$\log(p(Y_{ij}|\eta_i)) = -0.5 \log(2\pi\sigma^2) - \frac{(Y_{ij}-f(x_{ij}; \eta_i))^2}{2\sigma^2}$$ {#eq-likelihood-2}
Please note that in our case (a combined additive and proportional RUV model), $\sigma^2$ represents the combined variances at time $t_{ij}$ and prediction $f(x_{ij})$. As the structural solution of our model, $f(x_{ij})$, is a constant for a given $t_{ij}$, we can compute the combined variance as
$$\sigma^2 = \sigma^2_{prop} \cdot f(x_{ij})^2 + \sigma^2_{add}$$ {#eq-sigma2}
Therefore, we later have to calculate the $\sigma^2$ for each data point $Y_{ij}$ individually.
## Combining both terms {#sec-bayesth-map-final}
Writing out the log prior (@eq-prior-3) and log likelihood (@eq-likelihood-2) terms in our MAP estimation objective function (@eq-map-log), we obtain:
$$\eta_i^* = \underset{\eta_i}{\mathrm{argmax}}~\left(\left[-0.5 \log(2\pi\omega^2) - \frac{\eta_i^2}{2\omega^2}\right] ~ + \sum_{j=1}^m \left[-0.5 \log(2\pi\sigma^2) - \frac{(Y_{ij}-f(x_{ij}; \eta_i))^2}{2\sigma^2}\right]\right)$$ {#eq-map-final}
This final equation will guide our numerical optimizer (`optim` function in R) to determine the maximum, providing us with the individual MAP estimate. Let's implement this method in R and reproduce our NONMEM reference solution!
# R-based MAP reproduction {#sec-rrepro}
## Prior term {#sec-rrepro-prior}
We start by defining a function to calculate the prior term given by @eq-prior-3. Here, we simply pass the individual $\eta_i$ and the model parameters (including $\omega^2_{CL}$) as input arguments, and the function returns the log probability of the given $\eta_i$ under the prior distribution:
```{r filename="function: prior_fun()"}
#| echo: true
#| collapse: false
#| code-fold: false
# define prior term function
prior_fun <- function(eta_i, mod_par){
# retrieve omega2 from model parameters
omega2 <- mod_par$omega2_CL
# calculate probability
log_prob <- - 0.5 * log(2*pi*omega2) - eta_i^2/(2*omega2)
# return log probability
return(log_prob)
}
```
We can test this function by illustrating the prior term across a range of $\eta_i$ values:
```{r}
#| label: fig-prior-term
#| fig-cap: "Probability density of different random effects given a normal distribution centered around 0 with a variance of 0.11."
# define range
eta_i <- seq(-2, 2, 0.01)
# calculate prior term
prior <- prior_fun(eta_i = eta_i, mod_par = mod_par)
# create tibble
prior_tibble <- tibble(
eta_i = eta_i,
p = prior,
source = "prior"
)
# plot prior term
prior_tibble |>
ggplot(aes(x=eta_i, y=exp(p)))+
geom_line(color = "darkblue", linewidth = 0.8)+
geom_vline(xintercept = 0, linetype = "dashed", color = "darkblue", linewidth = 0.6)+
labs(
x = expression(eta[i]),
y = "Probability density",
title = "Prior term (random effect)"
)+
theme_bw()
```
The following plot shows how these $\eta_i$ values map onto the clearance domain:
```{r}
#| label: fig-prior-term-cl
#| fig-cap: "Probability density of different clearance values."
# plot prior term
prior_tibble |>
ggplot(aes(x=mod_par$tvcl*exp(eta_i), y=exp(p)))+
geom_line(color = "darkblue", linewidth = 0.8)+
geom_vline(xintercept = mod_par$tvcl, linetype = "dashed", color = "darkblue", linewidth = 0.6)+
labs(
x = expression(CL[i]),
y = "Probability density",
title = "Prior term (clearance)"
)+
theme_bw()
```
From the plots, we see that certain values of $\eta_i$ and $CL_i$ are more likely than others, based on our prior beliefs derived from the NLME model estimates, before observing any individual data. Let's continue with the likelihood term:
## Likelihood term {#sec-rrepro-likelihood}
To calculate the log likelihood term described in @eq-likelihood-2, we first have to define a model prediction function. Given our simple one-compartment model, we use a closed-form expression, though the principles apply equally to ODE-based models. More details on the model prediction function can be found in the previous blogpost, see @klose2025.
```{r filename="function: model_fun()"}
#| echo: true
#| collapse: false
#| code-fold: false
# define model function
model_fun <- function(eta_i, dose, vd, theta_tvcl, t) {
exp_eta_i <- exp(eta_i)
exponent <- -1 * (theta_tvcl * exp_eta_i / vd) * t
result <- (dose / vd) * exp(exponent)
return(result)
}
```
Next, we construct the likelihood function for individual observations. Please note that we have to calculate the $\sigma^2$ for each data point $Y_{ij}$ individually, as the variance contains an element proportional to the model prediction $f_i$ (see @eq-likelihood-2). The following equation calculates the log likelihood for a single observation:
```{r filename="function: log_likelihood_fun_single()"}
#| echo: true
#| collapse: false
#| code-fold: false
# define likelihood function for a single observation
log_likelihood_fun_single <- function(eta_i, dose, vd, theta_tvcl, t_ij, Y_ij, sigma2_add, sigma2_prop){
# get model predictions
f_ij <- model_fun(eta_i, dose, vd, theta_tvcl, t_ij)
# calculate resulting sigma2 for each timepoint (prop variance is scaled based on f_i^2)
sigma2 <- sigma2_prop * f_ij^2 + sigma2_add
# calculate probability
log_lik <- - 0.5 * log(2*pi*sigma2) - (Y_ij - f_ij)^2/(2*sigma2)
# return log likelihood
return(log_lik)
}
```
To illustrate this, we calculate the likelihood for each observation, then sum these to obtain the total likelihood for a given $\eta_i$. We demonstrate this using an example with $\eta_i = 0$:
```{r}
# calculate lok lik per row
sim_data_id5 <- sim_data_id5 |>
rowwise() |>
mutate(
log_lik = case_when(
EVID == 0 ~ log_likelihood_fun_single(
eta_i = 0,
dose = mod_par$dose,
vd = mod_par$tvvd,
theta_tvcl = mod_par$tvcl,
t_ij = TIME,
Y_ij = DV,
sigma2_add = mod_par$sigma2_add,
sigma2_prop = mod_par$sigma2_prop
),
EVID == 1 ~ NA_real_
)
) |>
ungroup() |>
mutate(
sum_log_lik = sum(log_lik, na.rm = TRUE)
)
# show sim_data_id5
sim_data_id5 |>
kable() |>
kable_styling()
```
We observe individual likelihood contributions and their sum. To streamline this process, we define a function that computes the summed likelihood across multiple observations:
```{r filename="function: log_likelihood_fun_multiple()"}
#| echo: true
#| collapse: false
#| code-fold: false
# define likelihood function for a set of observations
log_likelihood_fun_multiple <- function(df, eta_i, mod_par){
# retrieve information from mod_par
dose <- mod_par$dose
vd <- mod_par$tvvd
theta_tvcl <- mod_par$tvcl
sigma2_add <- mod_par$sigma2_add
sigma2_prop <- mod_par$sigma2_prop
# calculate log lik per row
log_lik_sum <- df |>
rowwise() |>
mutate(
log_lik = case_when(
EVID == 0 ~ log_likelihood_fun_single(
eta_i = eta_i,
dose = dose,
vd = vd,
theta_tvcl = theta_tvcl,
t_ij = TIME,
Y_ij = DV,
sigma2_add = sigma2_add,
sigma2_prop = sigma2_prop
),
EVID == 1 ~ NA_real_
)
) |>
ungroup() |>
pull(log_lik) |>
sum(na.rm = TRUE)
# return log likelihood sum
return(log_lik_sum)
}
```
Testing this function quickly confirms consistency of the obtained summed up likelihood with the previous result from the table (see above):
```{r}
# calculate likelihood
log_likelihood_fun_multiple(
df = sim_data_id5,
eta_i = 0,
mod_par = mod_par
)
```
Now, we can visualize the likelihood term across a range of $\eta_i$ values, similar to what we have did for the prior term:
```{r}
#| label: fig-likelihood-term
#| fig-cap: "Likelihood of different random effects given the observed datapoints of our exemplary individual."
# define range
eta_i <- seq(-2, 2, 0.01)
# empty list
ll_list <- list()
# loop over each element of eta_i
for(cur_eta_i in eta_i){
# calculate likelihood term
ll_list[[as.character(cur_eta_i)]] <- log_likelihood_fun_multiple(
df = sim_data_id5,
eta_i = cur_eta_i,
mod_par = mod_par
)
}
# convert to vector
ll_vector <- ll_list |> unlist() |> unname()
# create tibble
likelihood_tibble <- tibble(
eta_i = eta_i,
p = ll_vector,
source = "likelihood"
)
# plot likelihood term
likelihood_tibble |>
ggplot(aes(x=eta_i, y=exp(p)))+
geom_line(color = "darkred", linewidth = 0.8)+
geom_vline(xintercept = eta_i[which.max(ll_vector)], linetype = "dashed", color = "darkred", linewidth = 0.8)+
labs(
x = expression(eta[i]),
y = "Likelihood",
title = "Likelihood term"
)+
theme_bw()
```
The likelihood plot clearly indicates which $\eta_i$ values best describe the observed data. Identifying the maximum likelihood $\eta_i$ is straightforward:
```{r}
# get eta_i with highest likelihood
eta_i_max_likelihood <- eta_i[which.max(ll_vector)]
# show
eta_i_max_likelihood
```
The optimal $\eta_i$ value according to the likelihood term (and ignoring any prior information) is `r eta_i_max_likelihood`. Please note: As the likelihood is the product of many probabilities, each between 0 and 1, we typically deal with extremely small numerical values. Therefore, it is common practice to use logarithmic transformations for numerical stability. Next, we combine the prior and likelihood terms to perform MAP estimation.
## MAP estimation (posterior) {#map-rrepro-mapestim}
We now have to define an objective function for numerical optimization, combining prior and likelihood terms to estimate the posterior (as shown in @eq-map-final).
```{r filename="function: map_obj_fun()"}
#| echo: true
#| collapse: false
#| code-fold: false
# define MAP estimation objective function
map_obj_fun <- function(eta_i, df, mod_par){
# calculate log prior term
log_prior <- prior_fun(
eta_i = eta_i,
mod_par = mod_par
)
# calculate log likelihood term
log_likelihood <- log_likelihood_fun_multiple(
df = df,
eta_i = eta_i,
mod_par = mod_par
)
# combine both
log_posterior <- log_prior + log_likelihood
# return negative log posterior
return(-log_posterior)
}
```
Please note that we are returning the negative log posterior as it is easier to minimize a function than to maximize it. Using R's `optim` function, we estimate the MAP numerically. Here is the output form the `optim` call:
```{r}
# run optimization
map_est <- optim(
par = 0,
fn = map_obj_fun,
df = sim_data_id5,
mod_par = mod_par,
method = "BFGS"
)
# show estimation results
map_est
```
The resulting MAP estimate for $\eta_i$ is `r map_est$par`, closely matching the reference solution (`r nm_out$ETA1 |> unique()`) with an acceptable difference (`r format(map_est$par - (nm_out$ETA1 |> unique()), scientific = FALSE)`). Similarly to the other terms, we can visualize the posterior term across a range of $\eta_i$ values:
```{r}
#| label: fig-posterior-term
#| fig-cap: "The unnormalized posterior density."
# define range
eta_i <- seq(-2, 2, 0.01)
# empty list
post_list <- list()
# loop over each element of eta_i
for(cur_eta_i in eta_i){
# calculate likelihood term
post_list[[as.character(cur_eta_i)]] <- map_obj_fun(
eta_i = cur_eta_i,
df = sim_data_id5,
mod_par = mod_par
)
}
# convert to vector
post_vector <- post_list |> unlist() |> unname()
# create tibble
posterior_tibble <- tibble(
eta_i = eta_i,
p = -post_vector,
source = "posterior"
)
# plot likelihood term
posterior_tibble |>
ggplot(aes(x=eta_i, y=exp(p)))+
geom_line(color = "darkgreen", linewidth = 0.8)+
geom_vline(xintercept = map_est$par, linetype = "dashed", color = "darkgreen", linewidth = 0.8)+
labs(
x = expression(eta[i]),
y = "Unnormalized posterior density",
title = "Posterior distribution"
)+
theme_bw()
```
## Comparison of prior, likelihood, and posterior {#sec-map-rrepro-comp}
Finally, we compare the MAP estimate (mode of the posterior) with prior and likelihood terms visually:
```{r}
#| label: fig-comparison-prior-ll-post-term
#| fig-cap: "Comparison of prior, likelihood, and posterior."
# combine likelihood and prior
comp_tibble <- rbind(
prior_tibble,
likelihood_tibble,
posterior_tibble
) |>
mutate(source = factor(source, levels = c("prior", "posterior", "likelihood")))
# define linewidth
linewidth <- 0.8
# plot both distributions with different colors and fill
comp_tibble |>
ggplot(aes(x=eta_i, y=exp(p), fill = source, color = source))+
scale_x_continuous(breaks = c(-2,-1,0, signif(map_est$par,2), signif(eta_i_max_likelihood,2), 2))+
geom_line(linewidth = linewidth)+
geom_vline(
data = data.frame(source = factor("prior", levels = c("prior", "posterior", "likelihood"))),
aes(xintercept = 0),
color = "darkblue", linetype = "dashed", linewidth = linewidth
) +
geom_vline(
data = data.frame(source = factor("posterior", levels = c("prior", "posterior", "likelihood"))),
aes(xintercept = map_est$par),
color = "darkgreen", linetype = "dashed", linewidth = linewidth
) +
geom_vline(
data = data.frame(source = factor("likelihood", levels = c("prior", "posterior", "likelihood"))),
aes(xintercept = eta_i_max_likelihood),
color = "darkred", linetype = "dashed", linewidth = linewidth
) +
scale_color_manual(values = c(prior = "darkblue",
posterior = "darkgreen",
likelihood = "darkred")) +
facet_wrap(~source, scales = "free", ncol = 1)+
labs(
x = expression(eta[i]),
y = "(Unnormalized) probability density",
title = "Comparison of prior, likelihood, and posterior",
color = "Source"
) +
theme_bw() +
theme(legend.position = "none")
```
This clearly demonstrates how the posterior is influenced by both the prior and the likelihood, with the MAP estimate (mode of the posterior, green dashed line) reflecting a balance between these two sources of information.
# Conclusion {#map-rrepro-conclusion}
This simple example illustrates how to estimate the individual parameter $\eta_i$ (which translates to an individual clearance $CL_i$) for a single subject using a Bayesian approach. We have seen that the posterior distribution, often summarized by its mode (the MAP or EBE estimate), represents a compromise between the prior and the likelihood. This powerful technique enables the continuous integration of prior knowledge with new data and is very useful for many pharmacometric workflows. With that, I conclude this blog post and hope you enjoyed it. If you have any questions or feedback, please feel free to leave a comment.
[^1]: *MAP* estimates are also known as *Empirical Bayes Estimates* (EBE).
[^2]: Depending on the estimation algorithm.
[^3]: The dense sampling in combination with a simple additive error model for RUV led to a scenario where the posterior was nearly equal to the likelihood. Therefore, I have increased the additive error and introduced a proportional term as well. This places the posterior in the middle and I can recycle the old dataset I have simulated before.
[^4]: Actually, this took me quite some time to figure out. I was using the model from the previous blogpost, which only had an additive error and was missing the `INTERACTION` option (which doesn't matter if you are just using a constant additive error). With the newly introduced proportional error, I then had a mismatch between my calculations and the reference and I couldn't figure out why. The missing `INTERACTION` was the solution, as with the introduction of the proportional error the RUV does not remain constant (which NONMEM is assuming when `INTERACTION` is missing). Lesson learned!